The FERMI-DIRAC or MAXWELL-BOLTZMANN distribution functions are frequently
used to describe the distribution of carriers in equilibrium since they are
the solution of BOLTZMANN's transport equation for the case of vanishing applied electric field. In the
channel region of a MOSFET, however, the energy distribution deviates from the
ideal shape implied by expressions (3.15) or
(3.20). Carriers gain energy by the electric field in the channel,
and they experience scattering events. Models to describe the distribution
function of such hot carriers have been studied by numerous
authors [101,102,103]. One possibility to describe the
distribution of hot carriers is to use a heated MAXWELLian distribution
function
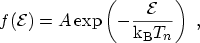 |
(3.24) |
where  denotes the electron temperature and
denotes the electron temperature and  is a normalization
constant. The validity of this approach, however, is limited.
Fig. 3.4 shows in the left part the contour lines of the heated
MAXWELLian distribution function at the Si-SiO
is a normalization
constant. The validity of this approach, however, is limited.
Fig. 3.4 shows in the left part the contour lines of the heated
MAXWELLian distribution function at the Si-SiO interface in comparison to
results3.4 for a MOSFET with a gate length of
interface in comparison to
results3.4 for a MOSFET with a gate length of
 nm and a thickness of the gate dielectric of 1.8nm at a bias of
nm and a thickness of the gate dielectric of 1.8nm at a bias of
 . It is evident that the heated MAXWELLian distribution
(full lines) yields only poor agreement with the results (dashed
lines). The distribution function at two points near the middle of the channel
(point A) and near the drain contact (point B) are shown in the right part of
this figure. Particularly the high-energy tail in the middle of the channel is
heavily overestimated by the heated MAXWELLian model. This is unsatisfactory
since a correct description of the high energy tail is crucial for the
evaluation of hot-carrier injection at the drain side used for programming and
erasing of EEPROM devices.
. It is evident that the heated MAXWELLian distribution
(full lines) yields only poor agreement with the results (dashed
lines). The distribution function at two points near the middle of the channel
(point A) and near the drain contact (point B) are shown in the right part of
this figure. Particularly the high-energy tail in the middle of the channel is
heavily overestimated by the heated MAXWELLian model. This is unsatisfactory
since a correct description of the high energy tail is crucial for the
evaluation of hot-carrier injection at the drain side used for programming and
erasing of EEPROM devices.
Figure 3.4:
Comparison of the heated MAXWELLian
distribution (full lines) with the results from a Monte Carlo simulation (dotted
lines) in a turned-on 180 nm MOSFET. Neighboring lines differ by a factor of
10. The distributions at point A and B are compared with a cold MAXWELLian
distribution in the right figure.
|
|
To obtain a better prediction of hot-carrier effects, CASSI and
RICCÓ presented an expression to account for the non-MAXWELL
ian shape of the electron energy distribution function [101]
 |
(3.25) |
with  as fitting parameter and
as fitting parameter and  being the local electric field in the
channel. This local-field dependence was soon questioned by other authors such
as FIEGNA et al. [104] who replaced the
electric field with an effective field calculated from the average electron
energy to model the EEPROM writing process. HASNAT et al.
used a similar form for the distribution function [105]
being the local electric field in the
channel. This local-field dependence was soon questioned by other authors such
as FIEGNA et al. [104] who replaced the
electric field with an effective field calculated from the average electron
energy to model the EEPROM writing process. HASNAT et al.
used a similar form for the distribution function [105]
 |
(3.26) |
They obtained values of  ,
,
 , and
, and
 by
fitting simulation results to measured gate currents. However, these values
fail to describe the shape of the distribution function along the channel when
compared to results [106]. A quite generalized approach for
the EED has been proposed by GRASSER et al.
by
fitting simulation results to measured gate currents. However, these values
fail to describe the shape of the distribution function along the channel when
compared to results [106]. A quite generalized approach for
the EED has been proposed by GRASSER et al.
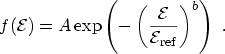 |
(3.27) |
In this expression the values of
 and
and  are mapped to the solution
variables
are mapped to the solution
variables  and
and  of a six moments transport model [107].
Expression (3.27) has been shown to appropriately reproduce
results in the source and the middle region of the channel of a turned-on
MOSFET. However, this model is still not able to reproduce the high energy
tail of the distribution function near the drain side of the channel because
it does not account for the population of cold carriers coming from the drain.
This was already visible in the right part Fig. 3.4 near the
drain side of the channel: The distribution consists of a cold MAXWELLian, a
high-energy tail, and a second cold MAXWELLian at higher
energies. Expression (3.27) cannot reproduce the low-energy MAXWELL
ian. A distribution function accounting for the cold carrier population near
the drain contact was proposed by SONODA et
al. [103], and an improved model has been suggested by
GRASSER et al. [106]:
of a six moments transport model [107].
Expression (3.27) has been shown to appropriately reproduce
results in the source and the middle region of the channel of a turned-on
MOSFET. However, this model is still not able to reproduce the high energy
tail of the distribution function near the drain side of the channel because
it does not account for the population of cold carriers coming from the drain.
This was already visible in the right part Fig. 3.4 near the
drain side of the channel: The distribution consists of a cold MAXWELLian, a
high-energy tail, and a second cold MAXWELLian at higher
energies. Expression (3.27) cannot reproduce the low-energy MAXWELL
ian. A distribution function accounting for the cold carrier population near
the drain contact was proposed by SONODA et
al. [103], and an improved model has been suggested by
GRASSER et al. [106]:
 |
(3.28) |
Here the pool of cold carriers in the drain region is correctly modeled by an
additional cold MAXWELLian subpopulation. The values of
 ,
,  , and
, and
 are again derived from the solution variables of a six moments transport
model [106]. Fig. 3.5 shows again the results from
simulations in comparison to the analytical model. A good match between
this non-MAXWELLian distribution and the results can be seen.
are again derived from the solution variables of a six moments transport
model [106]. Fig. 3.5 shows again the results from
simulations in comparison to the analytical model. A good match between
this non-MAXWELLian distribution and the results can be seen.
Figure 3.5:
Comparison of the non-MAXWELLian
distribution (full lines) with the results from a Monte Carlo simulation (dotted
lines) in a turned-on 180 nm MOSFET. Neighboring lines differ by a factor of
10. The distributions at point A and B are compared with a cold MAXWELLian
distribution in the right figure.
|
|
This model for the distribution function, however, requires to calculate the
third even moment of the distribution function, the kurtosis  . As an
approximation
. As an
approximation  can be calculated by an expression obtained for a bulk
semiconductor where a fixed relationship between
can be calculated by an expression obtained for a bulk
semiconductor where a fixed relationship between  ,
,  , and the
lattice temperature
, and the
lattice temperature
 exists:
exists:
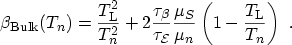 |
(3.29) |
In this expression
 ,
,
 ,
,  , and
, and  are the
energy relaxation time, the kurtosis relaxation time, the electron mobility,
and the energy flux mobility, respectively. The value of
are the
energy relaxation time, the kurtosis relaxation time, the electron mobility,
and the energy flux mobility, respectively. The value of
 can be approximated by a fit to
data [106]. Estimating the kurtosis from (3.29),
the distribution (3.27) can be used within the energy-transport or
hydrodynamic model. For a parabolic band structure, the expressions
can be approximated by a fit to
data [106]. Estimating the kurtosis from (3.29),
the distribution (3.27) can be used within the energy-transport or
hydrodynamic model. For a parabolic band structure, the expressions
 |
(3.30) |
 |
(3.31) |
are found [107], where  denotes the Gamma function
denotes the Gamma function
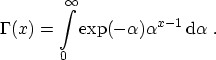 |
(3.32) |
While (3.30) can easily be inverted to obtain
 , the inversion of
(3.31) to find
, the inversion of
(3.31) to find  at
at
 cannot be given in a closed form. Instead, a fit expression
cannot be given in a closed form. Instead, a fit expression
 |
(3.33) |
with the parameters  =38.82,
=38.82,  =101.11,
=101.11,  =3.40, and
=3.40, and  =12.93 can
be used. Using
=12.93 can
be used. Using
 and
and  the distribution can be
approximated without knowledge of
the distribution can be
approximated without knowledge of  . Fig. 3.6 shows
simulation results for a 500nm MOSFET using the heated MAXWELLian
distribution (3.24), the non-MAXWELLian distribution
(3.28), and the non-MAXWELLian distribution (3.27) using
(3.30) and (3.33) to calculate the values of
. Fig. 3.6 shows
simulation results for a 500nm MOSFET using the heated MAXWELLian
distribution (3.24), the non-MAXWELLian distribution
(3.28), and the non-MAXWELLian distribution (3.27) using
(3.30) and (3.33) to calculate the values of
 and
and  . It can be
seen that the fit to the results from simulations is good. However, the
emerging population of cold carriers near the drain end of the channel leads
to a significant error in the shape of the distribution at low energy. This is
important for certain processes, while in the case of tunneling the
high-energy tail is more crucial.
. It can be
seen that the fit to the results from simulations is good. However, the
emerging population of cold carriers near the drain end of the channel leads
to a significant error in the shape of the distribution at low energy. This is
important for certain processes, while in the case of tunneling the
high-energy tail is more crucial.
With expression (3.27) for the distribution function and the
assumption of a FERMI-DIRAC distribution in the polysilicon gate, the supply
function (3.14) becomes
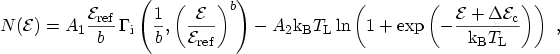 |
(3.34) |
where
 denotes the incomplete gamma
function
denotes the incomplete gamma
function
In (3.34) the explicit value of the FERMI energy was replaced by
the shift of the two conduction band edges
 . Assuming a MAXWELL
ian distribution in the polysilicon gate, the supply function can be further
simplified to
. Assuming a MAXWELL
ian distribution in the polysilicon gate, the supply function can be further
simplified to
 |
(3.35) |
Using the accurate shape of the distribution (3.28), the expressions
for the supply function become
for a FERMI-DIRAC distribution, and
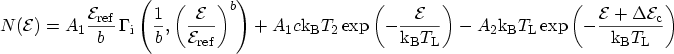 |
(3.36) |
assuming a MAXWELLian distribution in the polysilicon gate.
Figure 3.6:
The heated MAXWELLian distribution
(3.24), the non-MAXWELLian distribution (3.28), and
the non-MAXWELLian distribution (3.27) with (3.30) and (3.33)
compared to Monte Carlo results (from top to bottom).
|
|
A. Gehring: Simulation of Tunneling in Semiconductor Devices
![\includegraphics[width=0.54\linewidth]{figures/df_HM_MC}](img323.png)
![\includegraphics[width=0.45\linewidth]{figures/df_MD}](img324.png)
![]() and
and ![]() are mapped to the solution
variables
are mapped to the solution
variables ![]() and
and ![]() of a six moments transport model [107].
Expression (3.27) has been shown to appropriately reproduce
results in the source and the middle region of the channel of a turned-on
MOSFET. However, this model is still not able to reproduce the high energy
tail of the distribution function near the drain side of the channel because
it does not account for the population of cold carriers coming from the drain.
This was already visible in the right part Fig. 3.4 near the
drain side of the channel: The distribution consists of a cold MAXWELLian, a
high-energy tail, and a second cold MAXWELLian at higher
energies. Expression (3.27) cannot reproduce the low-energy MAXWELL
ian. A distribution function accounting for the cold carrier population near
the drain contact was proposed by SONODA et
al. [103], and an improved model has been suggested by
GRASSER et al. [106]:
of a six moments transport model [107].
Expression (3.27) has been shown to appropriately reproduce
results in the source and the middle region of the channel of a turned-on
MOSFET. However, this model is still not able to reproduce the high energy
tail of the distribution function near the drain side of the channel because
it does not account for the population of cold carriers coming from the drain.
This was already visible in the right part Fig. 3.4 near the
drain side of the channel: The distribution consists of a cold MAXWELLian, a
high-energy tail, and a second cold MAXWELLian at higher
energies. Expression (3.27) cannot reproduce the low-energy MAXWELL
ian. A distribution function accounting for the cold carrier population near
the drain contact was proposed by SONODA et
al. [103], and an improved model has been suggested by
GRASSER et al. [106]:
![\includegraphics[width=0.54\linewidth]{figures/df_SM_MC}](img336.png)
![\includegraphics[width=0.45\linewidth]{figures/df_MD2}](img337.png)
![]() . As an
approximation
. As an
approximation ![]() can be calculated by an expression obtained for a bulk
semiconductor where a fixed relationship between
can be calculated by an expression obtained for a bulk
semiconductor where a fixed relationship between ![]() ,
, ![]() , and the
lattice temperature
, and the
lattice temperature
![]() exists:
exists:
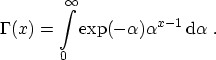


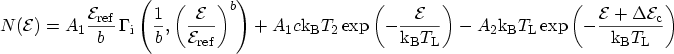
![\includegraphics[width=.50\linewidth]{figures/df3}](img362.png)