13.5.2 Second Order Space Convex

In the second order space convex scheme the equation

$$\phi_{ijk}^{n+1} = \phi_{ijk}^n - \Delta t \bigl( \max(F_{ijk},0) \nabla^+ + \min(F_{ijk},0) \nabla^- \bigr)$$

is the same as before, but $\nabla^+$ and $\nabla^-$ are different [44,87]. Here care is taken in the case of a shock by building an appropriate switch.

where

$$A := D_{ijk}^{-x} + \frac{\Delta x}{2} m( D_{ijk}^{-x-x}, D_{ijk}^{+x-x})$$

$$B := D_{ijk}^{+x} - \frac{\Delta x}{2} m( D_{ijk}^{+x+x}, D_{ijk}^{+x-x})$$

$$C := D_{ijk}^{-y} + \frac{\Delta y}{2} m( D_{ijk}^{-y-y}, D_{ijk}^{+y-y})$$

$$D := D_{ijk}^{+y} - \frac{\Delta y}{2} m( D_{ijk}^{+y+y}, D_{ijk}^{+y-y})$$

$$E := D_{ijk}^{-z} + \frac{\Delta z}{2} m( D_{ijk}^{-z-z}, D_{ijk}^{+z-z})$$

$$F := D_{ijk}^{+z} - \frac{\Delta z}{2} m( D_{ijk}^{+z+z}, D_{ijk}^{+z-z}).$$

The switch function 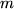$m$ is defined as

$$m(a,b):= \begin{cases} \begin{cases} x & \text{if $\vert x\vert\l... ...t$} \end{cases}& \text{if $xy\ge0$},\\ \quad 0 & \text{if $xy<0$}. \end{cases}$$

Figures 13.4 and 13.5 illustrate the comparison between these two schemes. Finally we note that schemes for non convex speed functions can be found in [88,1,2,4,121].

Figure 13.4: In this figure the first (red) and second order (black) space convex schemes are compared. Starting from a right angle at the inside the front is advanced by a constant speed function. Comparing both images one notices that the second order scheme can reproduce the quarter circle with less diffusion than the first order scheme.

Figure 13.5: Here the second order space convex scheme is used in the example of filling a V shaped structure with a right angle at the bottom. Again the front is advanced by a constant speed function. Both first and second order schemes can reproduce the corner correctly, which is not the case for the scheme that uses a forward difference for the time derivative and central differences for the spatial derivatives.