


 Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process
Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process
Although it is not relevant for the Monte-Carlo simulation of ion implantation it is
quite interesting to make some statements of the average nuclear stopping power.
Knowing the interatomic potential it is possible to derive the average nuclear
stopping power  which defines the average energy that is transfered by
each nuclear collisions if the particle energy is
which defines the average energy that is transfered by
each nuclear collisions if the particle energy is  .
.  can be
calculated by integrating the energy transfer
can be
calculated by integrating the energy transfer
 of a
nuclear collision event over all possible impact parameters
of a
nuclear collision event over all possible impact parameters  .
.
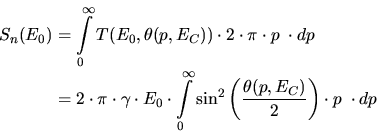 |
(3.93) |
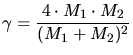 |
(3.94) |
Although there is no analytical solution for the average nuclear stopping power
 , a numerical solution can be derived using equations
(3.90), (3.89) and (3.88)
for the scattering angle
, a numerical solution can be derived using equations
(3.90), (3.89) and (3.88)
for the scattering angle
 [92]. Therefore the so called
dimensionless reduced energy
[92]. Therefore the so called
dimensionless reduced energy  and the dimensionless reduced nuclear
stopping have to be introduced.
and the dimensionless reduced nuclear
stopping have to be introduced.
The reduced energy considers the dependence of the nuclear stopping
power on the masses ( and
and  ) and the charges (
) and the charges ( and
and  ) of the
atoms involved in the scattering process. The relation between the real ion
energy
) of the
atoms involved in the scattering process. The relation between the real ion
energy  in units of keV and the reduced energy is given by
in units of keV and the reduced energy is given by
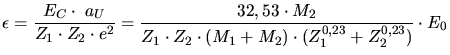 |
(3.95) |
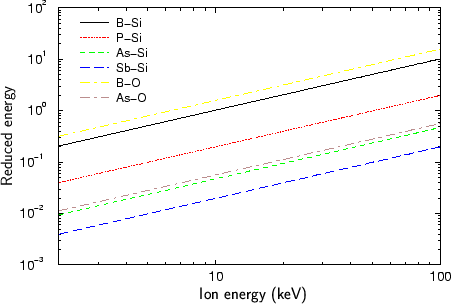
This relation is also plotted in in Fig. 3.6 for various atom pairs
relevant for semiconductor ion implantation to give an impression of the order
of the reduced energy.
Figure 3.6:
Reduced energy as function of the ion energy.
 |
The reduced nuclear stopping is defined by
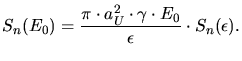 |
(3.96) |
It allows to find an analytical approximation to the numerical solution of the
nuclear stopping power. The analytical approximation for
 is
given by (3.97) and plotted in Fig. 3.7
[92].
is
given by (3.97) and plotted in Fig. 3.7
[92].
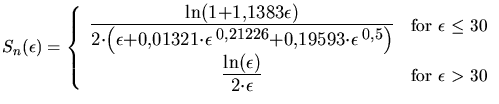 |
(3.97) |
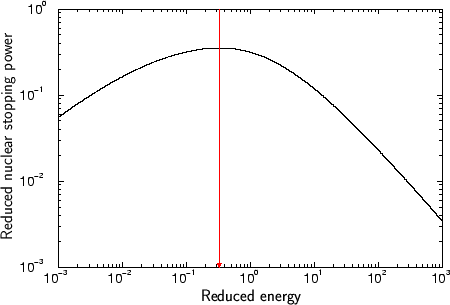
Figure 3.7:
Reduced nuclear stopping power as function of the reduced energy.
 |
Applying this approximation to (3.96) gives the
nuclear stopping power as expressed in (3.98) in units
of eV/(atom/cm ), by additionally inserting (3.94), (3.95)
and (3.92).
), by additionally inserting (3.94), (3.95)
and (3.92).
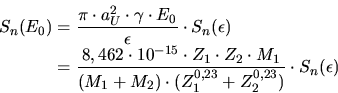 |
(3.98) |
 (3.97) has its maximum at a reduced
energy of
(3.97) has its maximum at a reduced
energy of  0,327 where also the average nuclear stopping power has its
maximum according to (3.98). The relating real particle
energy where the average stopping has is maximum can be calculated by
(3.95). Tab. 3.2 summarizes the approximate
stopping power maxima for various atom pairs.
0,327 where also the average nuclear stopping power has its
maximum according to (3.98). The relating real particle
energy where the average stopping has is maximum can be calculated by
(3.95). Tab. 3.2 summarizes the approximate
stopping power maxima for various atom pairs.
Table 3.2:
Maxima of the average nuclear stopping power for various atom pairs.
| Incident particle |
Target particle |
Nuclear stopping power maximum (keV) |
| Boron |
Silicon |
3 |
| Phosphorus |
Silicon |
16 |
| Arsenic |
Silicon |
68 |
| Antimony |
Silicon |
160 |
| Boron |
Oxygen |
2 |
| Phosphorus |
Oxygen |
12 |
| Arsenic |
Oxygen |
58 |
| Antimony |
Oxygen |
143 |
|



 Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process
Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
![]() which defines the average energy that is transfered by
each nuclear collisions if the particle energy is
which defines the average energy that is transfered by
each nuclear collisions if the particle energy is ![]() .
. ![]() can be
calculated by integrating the energy transfer
can be
calculated by integrating the energy transfer
![]() of a
nuclear collision event over all possible impact parameters
of a
nuclear collision event over all possible impact parameters ![]() .
.
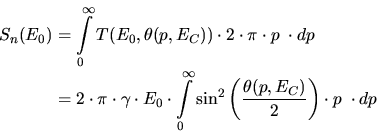
![]() , a numerical solution can be derived using equations
(3.90), (3.89) and (3.88)
for the scattering angle
, a numerical solution can be derived using equations
(3.90), (3.89) and (3.88)
for the scattering angle
![]() [92]. Therefore the so called
dimensionless reduced energy
[92]. Therefore the so called
dimensionless reduced energy ![]() and the dimensionless reduced nuclear
stopping have to be introduced.
and the dimensionless reduced nuclear
stopping have to be introduced.
![]() and
and ![]() ) and the charges (
) and the charges (![]() and
and ![]() ) of the
atoms involved in the scattering process. The relation between the real ion
energy
) of the
atoms involved in the scattering process. The relation between the real ion
energy ![]() in units of keV and the reduced energy is given by
in units of keV and the reduced energy is given by
![]()
![]()
![]()
![]() Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process
Previous: 3.3.2.1 Interatomic Screening Potential
Up: 3.3.2 Nuclear Stopping Process
Next: 3.3.3 Electronic Stopping Process