


 Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of
Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of
A solution of this problem was already given by Lindhard [50]. The
energy loss
 of the projectile is determined by the force
resulting from the electric field
of the projectile is determined by the force
resulting from the electric field
 which is generated in the
plasma by the penetrating charged particle with a charge
which is generated in the
plasma by the penetrating charged particle with a charge  moving with the
velocity
moving with the
velocity  . For his solution Lindhard applied the linear response theory.
. For his solution Lindhard applied the linear response theory.
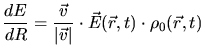 |
(3.100) |
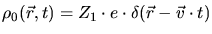 |
(3.101) |
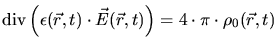 |
(3.102) |
 is the linear dielectric response function of the medium
on the charge.
is the linear dielectric response function of the medium
on the charge.
This set of differential equations can be solved by Fourier transformation
[50] (
 ).
).
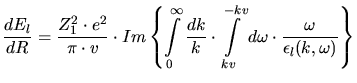 |
(3.103) |
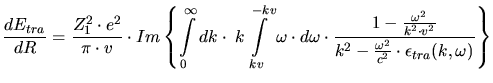 |
(3.104) |
The contributions to the energy loss by the transversal electric field
 and the longitudinal electric field
and the longitudinal electric field  are treated
separately, which requires the definition of a transversal
are treated
separately, which requires the definition of a transversal
 (Fourier transform of
(Fourier transform of
 )
and a longitudinal
)
and a longitudinal
 (Fourier transform of
(Fourier transform of
 ) dielectric response
function.
) dielectric response
function.
 and
and
 are defined
in Fourier space via the scalar potential
are defined
in Fourier space via the scalar potential
 and vector potential
and vector potential
 , describing the electromagnetic field as shown in
(3.105) and (3.106), and the Maxwell equations.
, describing the electromagnetic field as shown in
(3.105) and (3.106), and the Maxwell equations.
 |
(3.105) |
 |
(3.106) |
 is defined by
is defined by
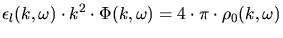 |
(3.107) |
while
 is defined by
is defined by
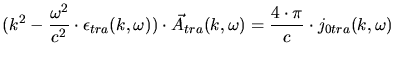 |
(3.108) |
The transversal field and the transversal current density are characterized by
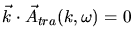 |
(3.109) |
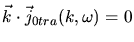 |
(3.110) |
The total energy loss is a sum of the longitudinal and the transversal
contribution, respectively. The transversal contribution is negligible since
the particle velocity is non-relativistic [50]. This requirement holds
for typical ion implantation conditions.
Lindhard derived an expression for the longitudinal dielectric response function
 by applying a self-consistent treatment of the electron
gas. He calculates the charge density
by applying a self-consistent treatment of the electron
gas. He calculates the charge density  and the current density
and the current density  induced in
the plasma by the forces resulting from the scalar potential
induced in
the plasma by the forces resulting from the scalar potential  and the
vector potential
and the
vector potential  . These induced sources produce an electro-magnetic
field which acts on the electron gas. Therefore the electro-magnetic field must
be self-consistent with the induced sources. A quantum-mechanical calculation of
this problem results in
. These induced sources produce an electro-magnetic
field which acts on the electron gas. Therefore the electro-magnetic field must
be self-consistent with the induced sources. A quantum-mechanical calculation of
this problem results in
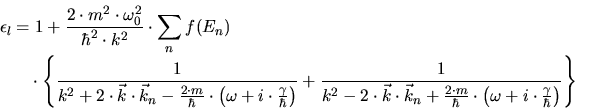 |
(3.111) |
with
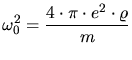 |
(3.112) |
being the classical resonance frequency of the gas.  is the electron density
distribution function,
is the electron density
distribution function,  is the electron mass,
is the electron mass,  is the energy,
is the energy,  the
wave vector of the electron in the nth state and
the
wave vector of the electron in the nth state and  is a small damping
factor. By applying this dielectric response function to
(3.103) Lindhard derived the energy loss in an electron gas
described by the Fermi distribution in the ground state with a maximum energy
is a small damping
factor. By applying this dielectric response function to
(3.103) Lindhard derived the energy loss in an electron gas
described by the Fermi distribution in the ground state with a maximum energy
 .
.
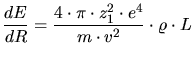 |
(3.113) |
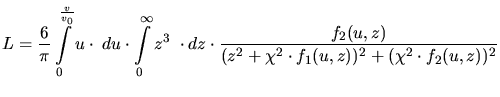 |
(3.114) |
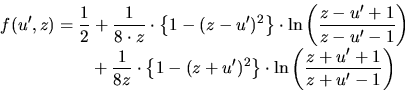 |
(3.115) |
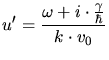 |
(3.116) |
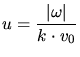 |
(3.117) |
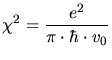 |
(3.118) |
Assuming a small damping factor  and a small particle
velocity
and a small particle
velocity  , (3.113) can be simplified to an electronic stopping
equation which is proportional to velocity.
, (3.113) can be simplified to an electronic stopping
equation which is proportional to velocity.
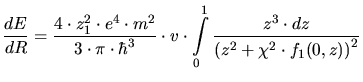 |
(3.119) |
 is the real part of (3.115), while
is the real part of (3.115), while  is the imaginary part.
is the imaginary part.



 Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of
Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
![]() of the projectile is determined by the force
resulting from the electric field
of the projectile is determined by the force
resulting from the electric field
![]() which is generated in the
plasma by the penetrating charged particle with a charge
which is generated in the
plasma by the penetrating charged particle with a charge ![]() moving with the
velocity
moving with the
velocity ![]() . For his solution Lindhard applied the linear response theory.
. For his solution Lindhard applied the linear response theory.
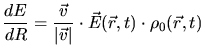
![]() ).
).
![]() and the longitudinal electric field
and the longitudinal electric field ![]() are treated
separately, which requires the definition of a transversal
are treated
separately, which requires the definition of a transversal
![]() (Fourier transform of
(Fourier transform of
![]() )
and a longitudinal
)
and a longitudinal
![]() (Fourier transform of
(Fourier transform of
![]() ) dielectric response
function.
) dielectric response
function.
![]() and
and
![]() are defined
in Fourier space via the scalar potential
are defined
in Fourier space via the scalar potential
![]() and vector potential
and vector potential
![]() , describing the electromagnetic field as shown in
(3.105) and (3.106), and the Maxwell equations.
, describing the electromagnetic field as shown in
(3.105) and (3.106), and the Maxwell equations.
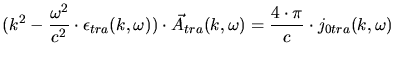
![]() by applying a self-consistent treatment of the electron
gas. He calculates the charge density
by applying a self-consistent treatment of the electron
gas. He calculates the charge density ![]() and the current density
and the current density ![]() induced in
the plasma by the forces resulting from the scalar potential
induced in
the plasma by the forces resulting from the scalar potential ![]() and the
vector potential
and the
vector potential ![]() . These induced sources produce an electro-magnetic
field which acts on the electron gas. Therefore the electro-magnetic field must
be self-consistent with the induced sources. A quantum-mechanical calculation of
this problem results in
. These induced sources produce an electro-magnetic
field which acts on the electron gas. Therefore the electro-magnetic field must
be self-consistent with the induced sources. A quantum-mechanical calculation of
this problem results in
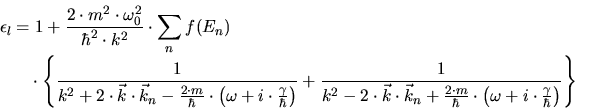
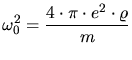
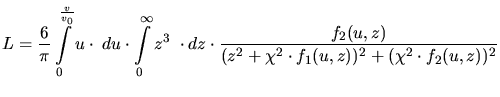
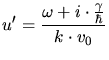
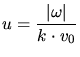
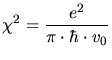
![]() and a small particle
velocity
and a small particle
velocity ![]() , (3.113) can be simplified to an electronic stopping
equation which is proportional to velocity.
, (3.113) can be simplified to an electronic stopping
equation which is proportional to velocity.
![]()
![]()
![]()
![]() Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of
Previous: 3.3.3 Electronic Stopping Process
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.3.2 Effective Charge of