


 Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -
Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -
3.3.4 Thermal Lattice Vibration
Although the wafer temperature during ion implantation is normally below 400 K,
the lattice vibrations can influence the trajectories of the implanted
ions. Especially the probability for scattering an ion out of a channel
(de-channeling) is increased by increasing
the wafer temperature. Due to the fact that the knowledge of the atomic
lattice behavior is required for the simulation it is necessary to apply a
temperature dependent lattice vibration model.
The thermal motion of the lattice atoms can be appropriately modeled by a
spherically symmetric Gaussian function
 which determines the
probability for finding an atomic core at the position
which determines the
probability for finding an atomic core at the position
 when the
corresponding lattice site is located at the origin.
when the
corresponding lattice site is located at the origin.
![$\displaystyle f(\vec{\Delta x}) = \frac{1}{\sqrt[3]{2\cdot \pi\cdot \sigma^2}}\cdot\exp\left( -\frac{\vert\vec{\Delta x}\vert^2}{2\cdot \sigma^2} \right)$](img397.gif) |
(3.139) |
The straggling of this distribution function can be modeled by the
Debye model of a solid [5].
![$\displaystyle \sigma^2 = 12,1\;\left[{\mathrm{\AA\sqrt{K}}}\right]\cdot\sqrt{\frac{\frac{x_D}{\Phi(x_D)} + \frac{1}{4}}{M_2\cdot \Theta_D}}$](img398.gif) |
(3.140) |
 |
(3.141) |
 |
(3.142) |
 is the relative mass of the atom of the solid. The Debye temperature
is the relative mass of the atom of the solid. The Debye temperature
 can be used as an empirical parameter, which can be determined for
instance by measurements of the specific heat or by channeling experiments
[17], [41] as summarized in
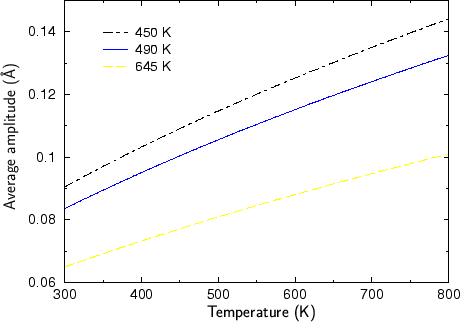
Tab. 3.4. Fig. 3.9 shows the average vibration
amplitude of silicon atoms as a function of the temperature for three different
Debye temperatures.
can be used as an empirical parameter, which can be determined for
instance by measurements of the specific heat or by channeling experiments
[17], [41] as summarized in
Tab. 3.4. Fig. 3.9 shows the average vibration
amplitude of silicon atoms as a function of the temperature for three different
Debye temperatures.
Table 3.4:
Experimentally determined Debye temperatures.
| Experimental method |
Debye temperature |
| Specific heat |
645 K |
| Channeling experiments [17] |
490 K |
| Implantation simulation [41] |
450 K |
|
Figure 3.9:
Amplitude of lattice vibration as a function of the temperature for
three Debye temperatures.
 |



 Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -
Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
![]() which determines the
probability for finding an atomic core at the position
which determines the
probability for finding an atomic core at the position
![]() when the
corresponding lattice site is located at the origin.
when the
corresponding lattice site is located at the origin.
![$\displaystyle f(\vec{\Delta x}) = \frac{1}{\sqrt[3]{2\cdot \pi\cdot \sigma^2}}\cdot\exp\left( -\frac{\vert\vec{\Delta x}\vert^2}{2\cdot \sigma^2} \right)$](img397.gif)
![$\displaystyle \sigma^2 = 12,1\;\left[{\mathrm{\AA\sqrt{K}}}\right]\cdot\sqrt{\frac{\frac{x_D}{\Phi(x_D)} + \frac{1}{4}}{M_2\cdot \Theta_D}}$](img398.gif)



![]()
![]()
![]()
![]() Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -
Previous: 3.3.3.3 Empirical Electronic Stopping
Up: 3.3 Monte-Carlo Method
Next: 3.3.5 Material Damage -