



Next: 5.3 Assembling and Solving
Up: 5. Discretization with the
Previous: 5.1 Basics
Subsections
5.2 Discretization with Tetrahedrons
An often used choice is to discretize the solution domain with tetrahedrons. On the one side a tetrahedron is a relative simple element, especially regarding meshing aspects, on the other side it is an efficient element to discretize structures with non-planar surfaces or complex geometries. As shown in Fig. 5.1, this element is limited by four triangles and has four vertexes which are in any case grid nodes in the mesh.
For using the weighted residual method the shape functions must be continuous on the transition from one element to its neighbor element. Within the elements they must be at least one-time differentiable. The shape functions will be defined locally on the tetrahedron. It should be noted that the global shape function
 is assembled from the local shape functions of the elements which share the same node
is assembled from the local shape functions of the elements which share the same node  .
.
If it is assumed that the discretization is carried out with linear shape functions, the four vertexes used are the four grid nodes on the element. This means that the shape functions must depend on the x-, y-, and z-coordinate linearly, so that in general form it can be expressed by [90]
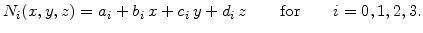 |
(5.8) |
 are the numbers of the local grid node. Since for every grid node a separate shape function is needed, there are four shape functions on a four node element. The coefficients
are the numbers of the local grid node. Since for every grid node a separate shape function is needed, there are four shape functions on a four node element. The coefficients  ,
,  ,
,  , and
, and  must be determined in such a manner, that the respective shape function
must be determined in such a manner, that the respective shape function  fulfills (5.4). This means, that for example the value of the shape function
fulfills (5.4). This means, that for example the value of the shape function  (x,y,z) must be 1 in node P
(x,y,z) must be 1 in node P with its coordinates (
with its coordinates ( ,
, ,
, ), and 0 in all other nodes. With this information the following equation system with N
), and 0 in all other nodes. With this information the following equation system with N on the four nodes can be written:
on the four nodes can be written:
With this equation system it is possible to determine the four unknown coefficients  ,
,  ,
,  , and
, and  for the shape function
for the shape function  (x,y,z).
(x,y,z).
Figure 5.1:
Tetrahedral element in a global  -coordinate system
-coordinate system
|
|
Figure 5.2:
Tetrahedral element in a normalized
 -coordinate system
-coordinate system
|
|
For calculation of the unknown coefficients Cramer's rule can be applied, which says: if there is an equation system
 , the numbers
, the numbers
 |
(5.10) |
are the components of the solution  .
.
With Cramer's rule, for example, the coefficient  from the shape function
from the shape function
 can be calculated by
can be calculated by
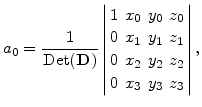 |
(5.11) |
where the matrix
 is
is
![$\displaystyle \mathbf{D}= \left[ \begin{array}{cccc} 1& x_0 &y_0 &z_0 1& x_1 &y_1 &z_1 1& x_2 &y_2 &z_2 1& x_3 &y_3 &z_3 \end{array} \right].$](img459.png) |
(5.12) |
By deleting the row i and the column j of a n-rowed determinant, a new (n-1)-rowed sub-determinant
 with sign
with sign
 is constructed
is constructed
 |
(5.13) |
To simplify the arithmetic, a n-rowed determinant can be calculated with the sum of n (n 1)-rowed sub-determinants (5.13). The determinant can be expanded from a row or column. If for example
1)-rowed sub-determinants (5.13). The determinant can be expanded from a row or column. If for example  is the number of any column, than the determinant is
is the number of any column, than the determinant is
 |
(5.14) |
With this rule (5.14) the coefficient  (5.11) can be simplified, because only
(5.11) can be simplified, because only
 , and the rest in the first column is 0. After expanding the determinant from the first row one obtains
, and the rest in the first column is 0. After expanding the determinant from the first row one obtains
 |
(5.15) |
In the same way all other coefficients of the shape function  can be determined
can be determined
 |
(5.16) |
The coefficients for the other shape functions can be found in the same way, the only difference leis in the equation system (5.9). Because, for example,
 must be 1 in node P
must be 1 in node P and 0 in all other nodes, it can be formulated
and 0 in all other nodes, it can be formulated
With the above described procedure also the coefficients for
 can be determined straightforwardly to
can be determined straightforwardly to
 |
(5.18) |
5.2.2 Coordinate Transformation
A coordinate transformation can help to simplify the calculation of integrals. For constructing the residual the calculation of the following element integral is frequently needed
 |
(5.19) |
Here the multiplication of two (linear) form functions leads to a more complex polynomial which complicates the integration over the region. It is more practical to integrate over a normalized element  (see Fig. 5.2). For this purpose, a tetrahedron with any location in the global (x,y,z)-coordinate system must be transformed into a normalized local
(see Fig. 5.2). For this purpose, a tetrahedron with any location in the global (x,y,z)-coordinate system must be transformed into a normalized local
 -coordinate system.
-coordinate system.
Each point (x,y,z) of the tetrahedral element in the global coordinate system can be transformed to a corresponding point
 in the normalized coordinate system with the following bijective projection rule
in the normalized coordinate system with the following bijective projection rule
This projection in matrix form leads to
 |
(5.21) |
and the conversion from the global to the normalized coordinates is
 |
(5.22) |
with
 and
and
 .
.
 is the so-called Jacobian matrix which only depends on the global coordinates (x,y,z)
is the so-called Jacobian matrix which only depends on the global coordinates (x,y,z)
![$\displaystyle \mathbf{J}= \left[ \begin{array}{ccc} x_1 - x_0 & \;x_2 - x_0 & \...
...y_0 & \;y_3 - y_0 z_1 - z_0 & \;z_2 - z_0 & \;z_3 - z_0 \end{array} \right].$](img485.png) |
(5.23) |
The element integral (5.19) calculated in the normalized coordinate system must be multiplied with the determinant of the Jacobian matrix
 |
(5.24) |
because the following relationship holds
 |
(5.25) |
The shape functions for the normalized tetrahedron  are simpler than those in the global coordinates, because they are reduced to [91]
are simpler than those in the global coordinates, because they are reduced to [91]
These shape functions lead to a simpler integrand in (5.24). A further advantage is that after normalization the lower integration limit is always 0, because as shown in Fig. 5.2, the tetrahedron  starts in the origin of ordinates.
starts in the origin of ordinates.
Also the upper limits can be found straightforwardly. As shown in Fig. 5.2, the element  is bounded by a plane which goes through the points P
is bounded by a plane which goes through the points P (1,0,0), P
(1,0,0), P (0,1,0), and P
(0,1,0), and P (0,0,1). This plane is described with the equation
(0,0,1). This plane is described with the equation
 .
The maximum on the
.
The maximum on the  -axes is 1. The limit in the
-axes is 1. The limit in the  -
- -plane (
-plane ( ) can be described with
) can be described with
 and the limit in
and the limit in  -direction is
-direction is
 .
.
With these limits the element integral of  can be written in the form
can be written in the form
 |
(5.27) |
This is a real advantage of the normalized tetrahedron, because there exists a simple scheme for  . The result from integration over the element
. The result from integration over the element  is either
is either
 or
or
 , only depending, if the two functions
, only depending, if the two functions  and
and  are equal or not. So in fact, to calculate the integral
are equal or not. So in fact, to calculate the integral  in the normalized coordinate system, only the determinant of the Jacobian matrix must be calculated. This procedure is much easier than to find the element integral for a common tetrahedron in the global coordinate system, where each element has a different size. This means that each integral
in the normalized coordinate system, only the determinant of the Jacobian matrix must be calculated. This procedure is much easier than to find the element integral for a common tetrahedron in the global coordinate system, where each element has a different size. This means that each integral  has a different result and must be calculated separately.
has a different result and must be calculated separately.
The differentiation of the whole projection (5.2.2), with respect to  leads to
leads to
with respect to  leads to
leads to
and with respect to  leads to
leads to
These derivatives can be also expressed in matrix form
![$\displaystyle \mathbf{I}=\mathbf{J}\times \left[ \begin{array}{ccc} \displaysty...
...partial y} &\displaystyle\frac{\partial \zeta}{\partial z} \end{array} \right],$](img517.png) |
(5.31) |
and the following relationship for the partial differential operators in the normalized system can be found with
![$\displaystyle \mathbf{J}^{-1}= \left[ \begin{array}{ccc} \displaystyle\frac{\pa...
...partial y} &\displaystyle\frac{\partial \zeta}{\partial z} \end{array} \right].$](img518.png) |
(5.32) |
The inverse of the Jacobian matrix (5.23) in the global coordinate system is given by
![$\displaystyle \mathbf{J}^{-1}= \frac{1}{\mathrm{Det}(\mathbf{J})} \left[ \begin...
... &L_{13} L_{21} &L_{22} &L_{23} L_{31} &L_{32} &L_{33} \end{array} \right],$](img519.png) |
(5.33) |
where the components  of the inverse matrix are
of the inverse matrix are
The components  of the Jacobian matrix (5.23) depend only on the location of the tetrahedron vertices in the global coordinate system. Because of
of the Jacobian matrix (5.23) depend only on the location of the tetrahedron vertices in the global coordinate system. Because of
 |
(5.35) |
there exists a relationship between the partial differential operators in the normalized system and the coordinates of the four nodes from the global system.
If any continuous function
 in the normalized coordinate system is differentiated in respect to
in the normalized coordinate system is differentiated in respect to  , then the chain rule must be used so that
, then the chain rule must be used so that
 |
(5.36) |
The gradient of the function
 in the normalized system becomes to
in the normalized system becomes to
![$\displaystyle \nabla f(\xi,\eta,\zeta)= \left[ \begin{array}{c} \displaystyle\...
...a} [2.8mm] \displaystyle\frac{\partial f}{\partial \zeta} \end{array} \right]$](img534.png) |
(5.37) |
This means that the gradient operator  in the normalized system must be multiplied with the transposed of the inverse Jacobian matrix
in the normalized system must be multiplied with the transposed of the inverse Jacobian matrix
![$\displaystyle \nabla=(\mathbf{J}^{-1})^\mathbf{T}\times\nabla^n= \frac{1}{\math...
...ta} [2.8mm] \displaystyle\frac{\partial }{\partial \zeta} \end{array} \right]$](img536.png) |
(5.38) |
5.2.4 Discretization of the Oxidant Diffusion
In the continuum formulation from (3.2), the diffusion of oxidants through the oxide material is described with
 |
(5.39) |
When Galerkin's method is applied, it is multiplied with a weight function
 and integrated over the domain
and integrated over the domain  , which leads to
, which leads to
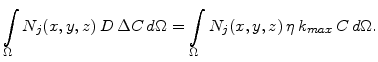 |
(5.40) |
If there are two functions
 and
and
 defined on a domain
defined on a domain  , Green's theorem says that
, Green's theorem says that
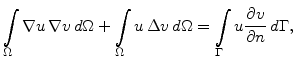 |
(5.41) |
where  is the boundary of the domain.
is the boundary of the domain.
With Green's theorem the Galerkin formulation from (5.40) can be rewritten in the form
 |
(5.42) |
Here the diffusion coefficient  and the maximal reaction rate
and the maximal reaction rate  do not directly depend on the location and, therefore, they do not need to be integrated over space and can stand outside of the integral. Furthermore, it is assumed that there is no flow of oxidants through the boundary surface and the boundary condition becomes
do not directly depend on the location and, therefore, they do not need to be integrated over space and can stand outside of the integral. Furthermore, it is assumed that there is no flow of oxidants through the boundary surface and the boundary condition becomes
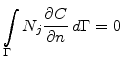 |
(5.43) |
With this Neumann boundary condition the Galerkin formulation for the oxidant diffusion can be reduced to
 |
(5.44) |
With the finite element method it can be assumed that this equation is only valid on a single tetrahedral element  . Furthermore, the scalar function for the oxidant concentration
. Furthermore, the scalar function for the oxidant concentration
 is here approximated linearly with
is here approximated linearly with
 |
(5.45) |
where
 is the value of the oxidant concentration in node
is the value of the oxidant concentration in node  and at discrete time
and at discrete time  .
.
 is the respective shape function from this node.
is the respective shape function from this node.
The distribution of the normalized silicon
 is approximated in the same way so that
is approximated in the same way so that
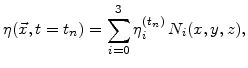 |
(5.46) |
where
 is the value of the normalized silicon in node
is the value of the normalized silicon in node  and at discrete time
and at discrete time  .
.
 is the linear shape function (5.8) for node
is the linear shape function (5.8) for node  .
.
With the approximation for
 and
and
 , the oxidant diffusion on a single element
, the oxidant diffusion on a single element  can be described with
can be described with
 |
(5.47) |
In the approximation for
 and
and
 the shape function
the shape function
 is the same. Since the values
is the same. Since the values  and
and  in the nodes do not depend on the spatial location, (5.47) can be rewritten as
in the nodes do not depend on the spatial location, (5.47) can be rewritten as
 |
(5.48) |
where it is assumed that
 .
.
By substituting the integrals with
the discretized equation for the oxidant diffusion is simplified to
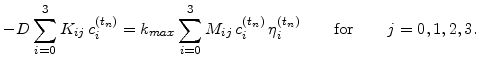 |
(5.50) |
The components  were already calculated in Section 5.2.2. After integration of
were already calculated in Section 5.2.2. After integration of
 in the normalized coordinate system, it was found that
in the normalized coordinate system, it was found that
 |
(5.51) |
For calculating the components  the integral is also transformed from the global to the normalized coordinate system, and with (5.25) follows
the integral is also transformed from the global to the normalized coordinate system, and with (5.25) follows
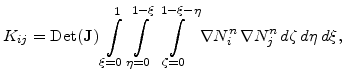 |
(5.52) |
where
 are the shape functions for a normalized tetrahedron
are the shape functions for a normalized tetrahedron  from (5.26).
from (5.26).
It was demonstrated in (5.38) that the transformation of the gradient operator  is carried out by a multiplication with the matrix
is carried out by a multiplication with the matrix
 , so that the integrand from (5.52) becomes
, so that the integrand from (5.52) becomes
After the multiplication of the two vectors and rearranging of this scalar product, (5.2.4) is
Here the  -terms which only depend on the location of the nodes in the global coordinate system, can be replaced by six constant coefficients
-terms which only depend on the location of the nodes in the global coordinate system, can be replaced by six constant coefficients 
With (5.55) the scalar product (5.54) can be simplified to
For example, the simplified scalar product (5.56) for  ,
,
 is
is
 |
(5.57) |
and for  ,
, 
 it is
it is
 |
(5.58) |
For all combinations of
 the simplified scalar product can be written in the form
the simplified scalar product can be written in the form
 |
(5.59) |
Instead of finding the scalar product (5.56), and the components of the matrices
 for all combinations of
for all combinations of
 by the way like in (5.57), it is more comfortable to use
by the way like in (5.57), it is more comfortable to use
![$\displaystyle \mathbf{N^n}= \left[ \begin{array}{c} 1-\xi-\eta-\zeta \xi \e...
...n{array}{c} -1 \phantom{-}0 \phantom{-}0 \phantom{-}1 \end{array}\right],$](img601.png) |
(5.60) |
and get the matrices
 with
with
![$\displaystyle \mathbf{S_A}=\frac{\partial \mathbf{N^n} }{\partial \xi}\times\Bi...
...}0 \phantom{-}0 &\phantom{-}0 &\phantom{-}0 &\phantom{-}0 \end{array}\right],$](img602.png) |
(5.61) |
![$\displaystyle \mathbf{S_B}= \left[ \begin{array}{c} -1 \phantom{-}1 \phant...
...ntom{-}0 &\phantom{-}0 &\phantom{-}0 &\phantom{-}0 \end{array}\right],\; \ldots$](img603.png) |
(5.62) |
Because the derivatives of the linear shape functions
 can only result in the values
can only result in the values  , 0 or
, 0 or  , the integral from (5.52) becomes
, the integral from (5.52) becomes
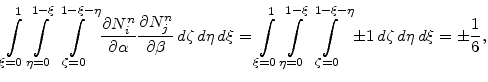 |
(5.63) |
which means that all matrices
 must be weighted with
must be weighted with
 .
.
After finding
 and integration over the (normalized) element, the coefficients
and integration over the (normalized) element, the coefficients  are
are
 |
(5.64) |
Galerkin's method assumes that the residual from the (discretized) equation of the oxidant diffusion is zero, and so (5.50) is rewritten in the form
 |
(5.65) |
This is a system with four equations, but with eight unknown variables
 and
and
 . Because of more unknowns than equations it is impossible to solve this equation system in present form. In the next section the required 4 equations introduced.
. Because of more unknowns than equations it is impossible to solve this equation system in present form. In the next section the required 4 equations introduced.
The dynamics of the normalized silicon concentration  in the continuum formulation (3.5) is described by
in the continuum formulation (3.5) is described by
 |
(5.66) |
After applying Galerkin's method with a weight function
 one obtains in a domain
one obtains in a domain  is
is
 |
(5.67) |
Because of the time dependence in this equation an additional time discretization of the term
 is necessary. This time discretization is performed with a simple backward-Euler method as
is necessary. This time discretization is performed with a simple backward-Euler method as
 |
(5.68) |
where  and
and  are two successive discrete times.
are two successive discrete times.
For an equation
 two Euler methods can be applied. The forward-Euler method is an explicit simple method, because the new value
two Euler methods can be applied. The forward-Euler method is an explicit simple method, because the new value
 is defined in terms of values that are already known [92].
The backward-Euler method comes from using
is defined in terms of values that are already known [92].
The backward-Euler method comes from using  at the end of a time step, when
at the end of a time step, when  . It is an implicit method, because in order to obtain the new discrete value
. It is an implicit method, because in order to obtain the new discrete value
 a linear equation of the form
a linear equation of the form
 must be solved [92], which requires additional computing time. But compared with the forward-Euler method the most important advantage of the backward-Euler method is that a much larger time step size
must be solved [92], which requires additional computing time. But compared with the forward-Euler method the most important advantage of the backward-Euler method is that a much larger time step size  can be used. The reason is that implicit methods are usually much more stable for solving a stiff equation. A stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the time step size is taken to be extremely small [93].
can be used. The reason is that implicit methods are usually much more stable for solving a stiff equation. A stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the time step size is taken to be extremely small [93].
The spatial approximation for the oxdiant concentration
 and the normalized silicon
and the normalized silicon
 for one finite element
for one finite element  is the same as in Section 5.2.4
is the same as in Section 5.2.4
With the time discretization (5.68) and the spatial approximation for
 and
and
 , the Galerkin formulation for the
, the Galerkin formulation for the  -dynamics on a finite element
-dynamics on a finite element  becomes
becomes
 |
(5.71) |
Because of the same shape function  for
for
 and
and
 and no spatial dependence of
and no spatial dependence of
 and
and
 , the last equation can be rearranged to
, the last equation can be rearranged to
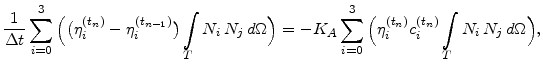 |
(5.72) |
After substituting
 from (5.51) the discretized equation for the
from (5.51) the discretized equation for the  -dynamics is simplified to
-dynamics is simplified to
 |
(5.73) |
In order to fulfill Galerkin's demand that the residual should be zero, the last equation can be rewritten as
 |
(5.74) |
which is also a system with four equations and eight unknown variables
 and
and
 . The values for
. The values for
 are already determined at the previous time step.
are already determined at the previous time step.
By combining the two equation systems (5.65) and (5.74), a non-linear but fully determined equation
system for one finite element, with 8 equations and the 8 unknowns
 and
and
 , is obtained. The system is non-linear because of the product
, is obtained. The system is non-linear because of the product
 in (5.65) and in (5.74). The complete equation system can be solved (for example with the Newton method) at each time point
in (5.65) and in (5.74). The complete equation system can be solved (for example with the Newton method) at each time point  and the values for
and the values for
 and
and
 can be determined.
can be determined.
The main interest in the continuum mechanics is the deformation of a body by internal or external forces. The deformation is expressed by the displacements  . The displacement of a point in a three-dimensional elastic continuum is defined by three displacement components
. The displacement of a point in a three-dimensional elastic continuum is defined by three displacement components  ,
,  , and
, and  in directions of the three coordinates
in directions of the three coordinates  ,
,  , and
, and  , so that
, so that
 |
(5.75) |
In contrast to the previous differential equations (5.39) and (5.66) for the mechanics Galerkin's method is not needed. Instead the virtual work concept is used [94]. The displacement components  ,
,  , and
, and  are directly discretized on a finite tetrahedral element
are directly discretized on a finite tetrahedral element
where  ,
,  , and
, and  are the displacement values in
are the displacement values in  -,
-,  -, and
-, and  -direction on node
-direction on node
 and
and  is the linear shape function from (5.8).
is the linear shape function from (5.8).
The strain components in the elastic case are first order derivatives of the displacement components
![$\displaystyle \tilde{\varepsilon}^e = \left\{ \begin{array}{c} \varepsilon_{xx}...
...B} \vec{d}^e=[\mathbf{B_0},\mathbf{B_1},\mathbf{B_2},\mathbf{B_3}] \vec{d^e}.$](img645.png) |
(5.77) |
The element displacement is defined by the 12 displacement components of the 4 nodes as
 |
(5.78) |
The submatrix
 of displacement derivatives for the node
of displacement derivatives for the node  is [95]
is [95]
![$\displaystyle \mathbf{B_i}= \left[ \begin{array}{ccc} \displaystyle{\frac{\part...
... d_i \;&0 \;&b_i \end{array} \right], \qquad \mathrm{where} \qquad i=0,1,2,3.$](img648.png) |
(5.79) |
The coefficients  ,
,  , and
, and  are the same as already presented in (5.16) and (5.18).
are the same as already presented in (5.16) and (5.18).
The entire inner virtual work on a continuous elastic body, and so also on a finite element is [94]
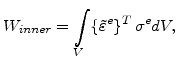 |
(5.80) |
with the stress tensor
 (3.15). Here it is assumed that there is no residual stress
(3.15). Here it is assumed that there is no residual stress
 , and the stress tensor is
, and the stress tensor is
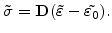 |
(5.81) |
In discretized form the transposed strain tensor is
 |
(5.82) |
After discretization the stress tensor (5.81) can be arranged as a function of the element displacement vector
 |
(5.83) |
Together with the transposed strain tensor (5.82), this stress tensor leads to the following discretized form of the equation for the inner virtual work on a finite element
 |
(5.84) |
The outer virtual work on a finite element, caused by the external nodal forces is
 |
(5.85) |
because it is assumed that during the oxidation process there are not external forces acting.
On any elastic body, and so also on a finite element, the inner work must be equal with the outer work
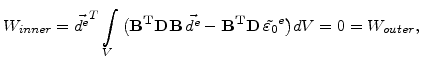 |
(5.86) |
which can be simplified to
 |
(5.87) |
Here the integrals can be substituted as sketched in [95]
where
 is the so-called stiffness matrix and
is the so-called stiffness matrix and
 can be declared as internal force vector. Since the integrands are not functions of the
can be declared as internal force vector. Since the integrands are not functions of the  -,
-,  -, or
-, or  -coordinates, the integration over the volume is equal with its much more simpler multiplication. The volume of any tetrahedron in the global coordinate system can be calculated with the determinant of matrix (5.12) by
-coordinates, the integration over the volume is equal with its much more simpler multiplication. The volume of any tetrahedron in the global coordinate system can be calculated with the determinant of matrix (5.12) by
 |
(5.90) |
The most important fact is that the residual strain tensor
 in (5.89) loads the mechanical system. Because the residual strain components
in (5.89) loads the mechanical system. Because the residual strain components
 are directly proportional to the normalized additional volume (3.37), there is a relationship between the volume expansion and the internal nodal forces.
are directly proportional to the normalized additional volume (3.37), there is a relationship between the volume expansion and the internal nodal forces.
With the integral substitutions (5.88) and (5.89), the balance equation (5.87) becomes a linear equation system for the mechanical problem on one finite element
 |
(5.91) |
The system is fully determined, because there are 12 equations and also 12 unknown displacement-components (three on each node) on the tetrahedron.




Next: 5.3 Assembling and Solving
Up: 5. Discretization with the
Previous: 5.1 Basics
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
![]() is assembled from the local shape functions of the elements which share the same node
is assembled from the local shape functions of the elements which share the same node ![]() .
.


![]() , the numbers
, the numbers
![]() from the shape function
from the shape function
![]() can be calculated by
can be calculated by
![]() in the normalized coordinate system with the following bijective projection rule
in the normalized coordinate system with the following bijective projection rule
![]() are simpler than those in the global coordinates, because they are reduced to [91]
are simpler than those in the global coordinates, because they are reduced to [91]
![]() is bounded by a plane which goes through the points P
is bounded by a plane which goes through the points P![]() (1,0,0), P
(1,0,0), P![]() (0,1,0), and P
(0,1,0), and P![]() (0,0,1). This plane is described with the equation
(0,0,1). This plane is described with the equation
![]() .
The maximum on the
.
The maximum on the ![]() -axes is 1. The limit in the
-axes is 1. The limit in the ![]() -
-![]() -plane (
-plane (![]() ) can be described with
) can be described with
![]() and the limit in
and the limit in ![]() -direction is
-direction is
![]() .
.
![]() can be written in the form
can be written in the form
![]() leads to
leads to
![$\displaystyle \mathbf{J}^{-1}= \frac{1}{\mathrm{Det}(\mathbf{J})} \left[ \begin...
... &L_{13} L_{21} &L_{22} &L_{23} L_{31} &L_{32} &L_{33} \end{array} \right],$](img519.png)

![]() in the normalized coordinate system is differentiated in respect to
in the normalized coordinate system is differentiated in respect to ![]() , then the chain rule must be used so that
, then the chain rule must be used so that

![]() and
and
![]() , the oxidant diffusion on a single element
, the oxidant diffusion on a single element ![]() can be described with
can be described with
![$\displaystyle \mathbf{N^n}= \left[ \begin{array}{c} 1-\xi-\eta-\zeta \xi \e...
...n{array}{c} -1 \phantom{-}0 \phantom{-}0 \phantom{-}1 \end{array}\right],$](img601.png)
![$\displaystyle \mathbf{S_A}=\frac{\partial \mathbf{N^n} }{\partial \xi}\times\Bi...
...}0 \phantom{-}0 &\phantom{-}0 &\phantom{-}0 &\phantom{-}0 \end{array}\right],$](img602.png)
![$\displaystyle \mathbf{S_B}= \left[ \begin{array}{c} -1 \phantom{-}1 \phant...
...ntom{-}0 &\phantom{-}0 &\phantom{-}0 &\phantom{-}0 \end{array}\right],\; \ldots$](img603.png)
![]() and integration over the (normalized) element, the coefficients
and integration over the (normalized) element, the coefficients ![]() are
are
![]() in the continuum formulation (3.5) is described by
in the continuum formulation (3.5) is described by
![]() two Euler methods can be applied. The forward-Euler method is an explicit simple method, because the new value
two Euler methods can be applied. The forward-Euler method is an explicit simple method, because the new value
![]() is defined in terms of values that are already known [92].
The backward-Euler method comes from using
is defined in terms of values that are already known [92].
The backward-Euler method comes from using ![]() at the end of a time step, when
at the end of a time step, when ![]() . It is an implicit method, because in order to obtain the new discrete value
. It is an implicit method, because in order to obtain the new discrete value
![]() a linear equation of the form
a linear equation of the form
![]() must be solved [92], which requires additional computing time. But compared with the forward-Euler method the most important advantage of the backward-Euler method is that a much larger time step size
must be solved [92], which requires additional computing time. But compared with the forward-Euler method the most important advantage of the backward-Euler method is that a much larger time step size ![]() can be used. The reason is that implicit methods are usually much more stable for solving a stiff equation. A stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the time step size is taken to be extremely small [93].
can be used. The reason is that implicit methods are usually much more stable for solving a stiff equation. A stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the time step size is taken to be extremely small [93].
![]() and the normalized silicon
and the normalized silicon
![]() for one finite element
for one finite element ![]() is the same as in Section 5.2.4
is the same as in Section 5.2.4
![]() and
and
![]() , is obtained. The system is non-linear because of the product
, is obtained. The system is non-linear because of the product
![]() in (5.65) and in (5.74). The complete equation system can be solved (for example with the Newton method) at each time point
in (5.65) and in (5.74). The complete equation system can be solved (for example with the Newton method) at each time point ![]() and the values for
and the values for
![]() and
and
![]() can be determined.
can be determined.
![]() . The displacement of a point in a three-dimensional elastic continuum is defined by three displacement components
. The displacement of a point in a three-dimensional elastic continuum is defined by three displacement components ![]() ,
, ![]() , and
, and ![]() in directions of the three coordinates
in directions of the three coordinates ![]() ,
, ![]() , and
, and ![]() , so that
, so that