The use of
 in microelectronic devices is very convenient because
in microelectronic devices is very convenient because
 builds a native oxide on top of the
builds a native oxide on top of the
 surface following the oxidation reactions
surface following the oxidation reactions
where the
 is built by
is built by
 consumption from the surface. After the
first oxide layer is built, oxygen and water have to diffuse to the
consumption from the surface. After the
first oxide layer is built, oxygen and water have to diffuse to the
 -
-
 interface to grow new oxide.
With this type of oxidation, very thin layers of
interface to grow new oxide.
With this type of oxidation, very thin layers of
 can be deposited.
However, thick oxide layers take a long time to build with this process
technique and use a certain amount of
can be deposited.
However, thick oxide layers take a long time to build with this process
technique and use a certain amount of
 as a source of the oxide layer.
as a source of the oxide layer.
Therefore, another technique has been introduced which transports all its
sources via a carrier gas to the reactor where they react at the wafer surface,
using the wafer surface as a catalytic material.
A deposition process using silane
 has been commonly established, which
follows the reaction equation
has been commonly established, which
follows the reaction equation
 |
(2.140) |
where the
 reacts with oxygen at the hot wafer surface and
reacts with oxygen at the hot wafer surface and
 is built together with
is built together with
 . A optimal temperature for this reaction
process is in the region of 1300 K [25].
The by-products from (2.138)-(2.140) are able to
diffuse through the oxide to the plain
. A optimal temperature for this reaction
process is in the region of 1300 K [25].
The by-products from (2.138)-(2.140) are able to
diffuse through the oxide to the plain
 and react with
and react with
 as oxygen or
as water according to (2.138) and (2.139).
This diffusion of oxygen and water can be controlled by regulating the
temperature of the reaction process (2.140). However, despite of the
regulative measures, some of the
as oxygen or
as water according to (2.138) and (2.139).
This diffusion of oxygen and water can be controlled by regulating the
temperature of the reaction process (2.140). However, despite of the
regulative measures, some of the
 is alway consumed.
In addition, a considerable concentration of
is alway consumed.
In addition, a considerable concentration of
 is built during the
deposition of
is built during the
deposition of
 and has to be taken into account for reliability issues
during the further processing and the device operations [25,127].
and has to be taken into account for reliability issues
during the further processing and the device operations [25,127].
The previously presented methods have shown how a
 layer can be deposited by
using
layer can be deposited by
using
 from the target material (wafer). However, if
from the target material (wafer). However, if
 consumption
is not allowed at the surface, a more complex deposition method is required. A
possible alternative, which provides that requirement is TEOS
(Tetra-ethoxy-silane,
consumption
is not allowed at the surface, a more complex deposition method is required. A
possible alternative, which provides that requirement is TEOS
(Tetra-ethoxy-silane,
 ). The deposition of
). The deposition of
 with TEOS uses a
pyrolytic chemical reaction at a hot wafer surface in a LPCVD process
(low pressure chemical vapor deposition)
and follows the chemical reaction [25,127]
with TEOS uses a
pyrolytic chemical reaction at a hot wafer surface in a LPCVD process
(low pressure chemical vapor deposition)
and follows the chemical reaction [25,127]
 |
(2.141) |
where the semiconductor device structures on the wafer are heated at a
temperature of approximately  K. The reactant TEOS is transported
from a material reservoir to the reactor via a carrier gas typically consisting
of
K. The reactant TEOS is transported
from a material reservoir to the reactor via a carrier gas typically consisting
of
 and
and
 .
At the hot surface of the wafer, the pyrolytic dissociation reaction (2.141)
takes place. Typical
.
At the hot surface of the wafer, the pyrolytic dissociation reaction (2.141)
takes place. Typical
 growth rates at these environment conditions are
100 Å/min [25] up to 1000 Å/min [127]. The growth
rate can be controlled within a certain range by varying the temperature,
pressure, and the TEOS concentration in the carrier gas.
Typically, the deposition reactions follow an ARRHENIUS2.38law [176]
growth rates at these environment conditions are
100 Å/min [25] up to 1000 Å/min [127]. The growth
rate can be controlled within a certain range by varying the temperature,
pressure, and the TEOS concentration in the carrier gas.
Typically, the deposition reactions follow an ARRHENIUS2.38law [176]
 |
(2.142) |
where the reaction rate  depends exponentially on the activation energy
depends exponentially on the activation energy
 . The proportionality constant
. The proportionality constant  depends on the surface shape and the
chemical reaction which takes place and must therefore be determined separately
for each different deposition type.
The proportionality constant
depends on the surface shape and the
chemical reaction which takes place and must therefore be determined separately
for each different deposition type.
The proportionality constant  often depends on the temperature through a
square-root law [127]
often depends on the temperature through a
square-root law [127]
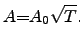 |
(2.143) |
Stefan Holzer
2007-11-19
![]() in microelectronic devices is very convenient because
in microelectronic devices is very convenient because
![]() builds a native oxide on top of the
builds a native oxide on top of the
![]() surface following the oxidation reactions
surface following the oxidation reactions
![]() has been commonly established, which
follows the reaction equation
has been commonly established, which
follows the reaction equation
![]() layer can be deposited by
using
layer can be deposited by
using
![]() from the target material (wafer). However, if
from the target material (wafer). However, if
![]() consumption
is not allowed at the surface, a more complex deposition method is required. A
possible alternative, which provides that requirement is TEOS
(Tetra-ethoxy-silane,
consumption
is not allowed at the surface, a more complex deposition method is required. A
possible alternative, which provides that requirement is TEOS
(Tetra-ethoxy-silane,
![]() ). The deposition of
). The deposition of
![]() with TEOS uses a
pyrolytic chemical reaction at a hot wafer surface in a LPCVD process
(low pressure chemical vapor deposition)
and follows the chemical reaction [25,127]
with TEOS uses a
pyrolytic chemical reaction at a hot wafer surface in a LPCVD process
(low pressure chemical vapor deposition)
and follows the chemical reaction [25,127]
