Next: 3.4 Heat Capacitance Up: 3. Thermal Models Previous: 3.2 Electrical Permittivity Contents
According to FOURIER's law (e.g. to Chapter 2)
the heat flow between two regions having different temperatures is
determined by the temperature gradient and a proportional factor ![]() .
The value of the thermal conductivity for metals is related to
the electrical conductivity because the electron gas in the metal transports the
heat as well as the electrical current.
WIEDEMANN and FRANZ found that the ratio between the electrical and
thermal conductivity for a metal is proportional to the absolute temperature
.
The value of the thermal conductivity for metals is related to
the electrical conductivity because the electron gas in the metal transports the
heat as well as the electrical current.
WIEDEMANN and FRANZ found that the ratio between the electrical and
thermal conductivity for a metal is proportional to the absolute temperature
| Material | References | |
| Si Nanowires |
|
[77,78] |
| Diamond |
|
[79] |
| Cu |
|
[191,39] |
|
|
[191,39] | |
|
|
[191,39] | |
|
|
[191,39] | |
| Al |
|
[33] |
|
|
[33] | |
|
|
[33] | |
|
|
[33] | |
| n-polySi |
|
[192,193,194,80,195] |
| p-polySi |
|
[194] |
| Si |
|
[79,136] |
|
|
[79,136] | |
|
|
[79,136] | |
|
|
[79,136] | |
| Ge |
|
[79,136] |
|
|
[79,136] | |
|
|
[79,136] | |
|
|
[79,136] | |
| GaAs |
|
[79] |
|
|
[25] | |
|
|
[25] |
| (3.18) |
| (3.19) |
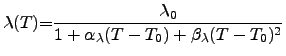 |
(3.20) |
As a first approach the thermal conductivity can be assumed to follow the WIEDEMANN-FRANZ-LORENZ law, also for nonmetalic materials. However, to improve the model accuracy for semiconducting and insulating materials, a polynomial model may be used. A comparison of typical values of the thermal conductivities of common materials is given in Tab. 3.3 and Figure 2.9, where Tab. 3.3 shows a list of common materials ordered by descending thermal conductivities and Figure 2.9 gives an overview of the temperature dependence of various materials compared to Si and Ge.