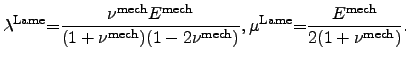If several materials are combined within a microstructure, mechanical forces
occur if the volumes of the different materials change. Several effects
may enforce volume expansion, for instance chemical reactions, phase
interchanges and recrystallization, mass migration, and thermal expansion and
contraction.
In this thesis, the mechanical stress due to thermal expansion is considered.
The mechanical stress
 can be separated into a static and a thermal
stress component [33] as
can be separated into a static and a thermal
stress component [33] as
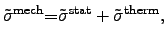 |
(3.23) |
where
 represents the static stress component, which is
impressed and mostly fixed by the fabrication processes, for instance material
deposition, annealing, and packaging.
The thermal component of the stress
represents the static stress component, which is
impressed and mostly fixed by the fabrication processes, for instance material
deposition, annealing, and packaging.
The thermal component of the stress
 is a transient
quantity influenced by the ambient temperature and other
state variables of the system. The corresponding hydrostatic pressure
is a transient
quantity influenced by the ambient temperature and other
state variables of the system. The corresponding hydrostatic pressure
 is then defined as the trace of the mechanical stress tensor
is then defined as the trace of the mechanical stress tensor
 ,
,
 for for |
(3.24) |
which represents an averaged value and can be used for significant comparisons,
as a figure of merit for optimization purposes, and to visualize the mechanical
stress in a microelectronic device structure.
The local force density which acts on the material can be described by the
mechanical stress tensor
 , which can be derived from the mechanical
strain tensor
, which can be derived from the mechanical
strain tensor
 using the LAMÉ3.4 formalism to model
(2.109) as
using the LAMÉ3.4 formalism to model
(2.109) as
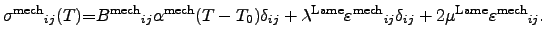 |
(3.25) |
The quantities
 and
and
 are the LAMÉ constants, which can be
expressed by YOUNG's modulus
are the LAMÉ constants, which can be
expressed by YOUNG's modulus
 and POISSON's ratio
and POISSON's ratio
 [96,97] as
[96,97] as
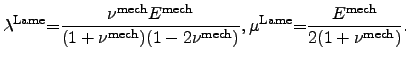 |
(3.26) |
For orthotropic materials the number of independent components for the stiffness and stress tensor is
reduced due to energetic considerations and symmetry in the
crystals [202,96,97].
Hence, the number of independent components of the stiffness tensor (forth rank)
is reduced to nine and for the stress tensor (second rank) to six. Hence,
the mechanical problem can be expressed in terms of vectors and
matrices [202] according to the VOIGT notation.
Stefan Holzer
2007-11-19
![]() can be separated into a static and a thermal
stress component [33] as
can be separated into a static and a thermal
stress component [33] as
 for
for![]() , which can be derived from the mechanical
strain tensor
, which can be derived from the mechanical
strain tensor
![]() using the LAMÉ3.4 formalism to model
(2.109) as
using the LAMÉ3.4 formalism to model
(2.109) as