



Next: Bibliography
Up: E. Diffraction in Far
Previous: E.2 Circular Aperture
E.3 Rectangular Aperture
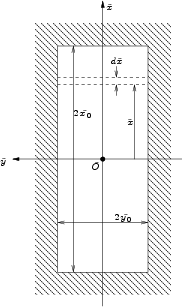
Figure E.6 shows the aperture plane with
the coordinates  and
and  .
.
Figure E.6:
Coordinate system in a rectangular aperture
 |
The transmission function is
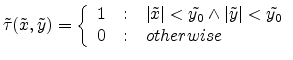 |
(E.54) |
The area of the aperture is given by
 . The
FOURIER transform can be calculated from
(E.27) and splitted into two integrals
. The
FOURIER transform can be calculated from
(E.27) and splitted into two integrals
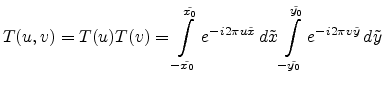 |
(E.55) |
One stripe in Figure E.6 is thereby
given by
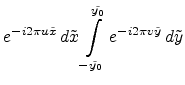 |
(E.56) |
Integration of (E.55) is simple and
straightforward
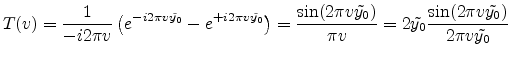 |
(E.57) |
The rightmost term can be defined as a new function
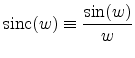 |
(E.58) |
With this substitution (E.57)
yields
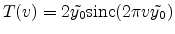 |
(E.59) |
and
 |
(E.60) |
in an analogous way.
Therefore in Point  the electric field is according to
(E.29)
the electric field is according to
(E.29)
![$\displaystyle E'(u,v) = E'(0,0)\frac{2x_0 \sinc (2\pi u\tilde{x_0})2y_0\sinc (2...
...0}\tilde{y_0}}\left[\frac{R_{00}R'_{00}}{R_0R'_0}\right]e^{i(\phi_0-\phi_{00})}$](img607.png) |
|
![$\displaystyle = E'(0,0) \sinc (2\pi u\tilde{x_0})\sinc (2\pi \tilde{y_0})\left[\frac{R_{00}R'_{00}}{R_0R'_0}\right]e^{i(\phi_0-\phi_{00})}$](img608.png) |
(E.61) |
and the intensity as the square of the electrical field is then
![$\displaystyle I'(u,v) = I'(0,0) \sinc ^2(2\pi u \tilde{x_0}) \sinc ^2(2\pi v\tilde{y_0})\left[\frac{R_{00}R'_{00}}{R_0R'_0}\right]^2$](img609.png) |
(E.62) |
For the special case of the source being located on the z-axis, the
coordinates  are zero and the coordinates
are zero and the coordinates  are the following
functions of
are the following
functions of 
 and and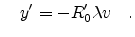 |
(E.63) |
For  and
and  (the direct beam) the coordinates are
(the direct beam) the coordinates are  and according to
(E.63)
and according to
(E.63)  . The direct beam is therefore
in the z-axis and
. The direct beam is therefore
in the z-axis and
 can be written as
can be written as
Together with (E.14) and
(E.64) the square of the fraction in
(E.62) gives
Therefore this fraction can be set to unity if
 .
This assumption yields finally for the intensity behind a rectangular aperture
.
This assumption yields finally for the intensity behind a rectangular aperture
Figure E.7:
Comparison of different intensity distributions after diffraction
at a rectangular aperture (a) square aperture (b) detail of
square aperture (c) rectangular aperture with
 (d) rectangular aperture with
(d) rectangular aperture with

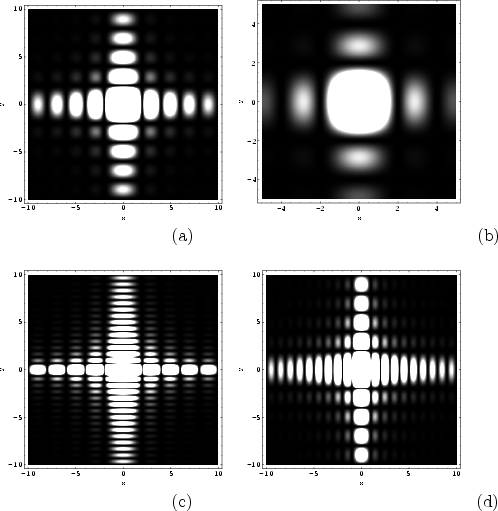 |




Next: Bibliography
Up: E. Diffraction in Far
Previous: E.2 Circular Aperture
R. Minixhofer: Integrating Technology Simulation
into the Semiconductor Manufacturing Environment

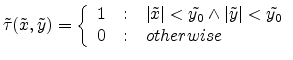
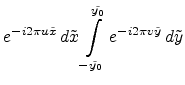
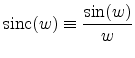
![$\displaystyle E'(u,v) = E'(0,0)\frac{2x_0 \sinc (2\pi u\tilde{x_0})2y_0\sinc (2...
...0}\tilde{y_0}}\left[\frac{R_{00}R'_{00}}{R_0R'_0}\right]e^{i(\phi_0-\phi_{00})}$](img607.png)
![$\displaystyle = E'(0,0) \sinc (2\pi u\tilde{x_0})\sinc (2\pi \tilde{y_0})\left[\frac{R_{00}R'_{00}}{R_0R'_0}\right]e^{i(\phi_0-\phi_{00})}$](img608.png)
![]() are zero and the coordinates
are zero and the coordinates ![]() are the following
functions of
are the following
functions of ![]()



