



Next: 3.3.5 Effective Density of
Up: 3.3 Band-Structure
Previous: 3.3.3 Bandgap Narrowing
3.3.4 Effective Carrier Mass
In this work, parabolic conduction and valence bands are assumed, and the
effects of band non-parabolicity are assumed to be negligible. Therefore,
effective masses for each of the three conduction band minima ( , X, and
L) can be defined and used to calculate the density of states (DOS). The DOS
in the valence band can be characterized by the effective masses of three
sub-bands, all in the center of the Brillouin zone: two degenerate
sub-bands of light and heavy holes, and the split-off sub-band. The
contribution of the split-off band, which is depressed in energy and is much
less populated, is neglected in this work.
, X, and
L) can be defined and used to calculate the density of states (DOS). The DOS
in the valence band can be characterized by the effective masses of three
sub-bands, all in the center of the Brillouin zone: two degenerate
sub-bands of light and heavy holes, and the split-off sub-band. The
contribution of the split-off band, which is depressed in energy and is much
less populated, is neglected in this work.
The effective DOS masses scaled by the free electron mass give relative carrier
masses. In materials with direct bandgap the
value of the relative mass for electrons from the  valley is
considered. In the case of materials with indirect bandgaps namely Si, Ge,
AlAs, and GaP the transverse and the longitude electron masses (
valley is
considered. In the case of materials with indirect bandgaps namely Si, Ge,
AlAs, and GaP the transverse and the longitude electron masses (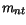 and
and
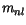 ) from the X valley (respectively L valley for Ge) are taken into account by
(3.86). For all materials the hole masses are calculated by
(3.87) accounting for the heavy and the light hole masses (
) from the X valley (respectively L valley for Ge) are taken into account by
(3.86). For all materials the hole masses are calculated by
(3.87) accounting for the heavy and the light hole masses (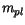 and
and 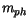 ) [86].
) [86].
The model parameters 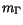 ,
, 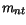 ,
, 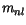 ,
, 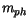 , and
, and 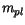 are summarized in Table 3.16. In addition, the calculated values
for
are summarized in Table 3.16. In addition, the calculated values
for  and
and 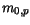 are included, after comparison to calculated values
reported in literature.
are included, after comparison to calculated values
reported in literature.
Table 3.16:
Parameter values for modeling the effective carrier masses
| Material |
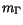 |
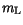 |
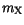 |
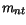 |
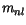 |
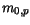 |
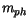 |
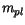 |
References |
| Si |
|
|
0.328 |
0.19 |
0.98 |
0.55 |
0.49 |
0.16 |
[90,86,85] |
| Ge |
|
0.222 |
0.42 |
0.082 |
1.64 |
0.28 |
0.29 |
0.04 |
[90,86,85,94] |
| GaAs |
0.067 |
|
0.471 |
0.229 |
1.987 |
0.49 |
0.49 |
0.08 |
[117,86,115,150] |
| AlAs |
0.15 |
|
0.38 |
0.19 |
1.5 |
0.81 |
0.76 |
0.16 |
[108,71] |
| InAs |
0.023 |
|
0.64 |
0.271 |
3.619 |
0.41 |
0.41 |
0.025 |
[86,85,88,94] |
| InP |
0.077 |
|
0.462 |
0.273 |
1.321 |
0.64 |
0.6 |
0.12 |
[108,71,92,94] |
| GaP |
0.15 |
|
0.5 |
0.25 |
1.993 |
0.6 |
0.79 |
0.14 |
[85,94,73,91] |
|
The temperature dependence of the relative carrier masses is well studied in
the case of Si (see [120] and references therein). However, for
III-V materials such data are scattering or missing and the effect is often
neglected. A linear temperature dependence (3.88) is sufficient to model
the relative electron masses for all materials [151]. A quadratic
temperature dependence model (3.89) is introduced for the relative hole
masses, as the simplest expression sufficient to fit well the data for Si.
Table 3.17 summarizes the values of the model parameters. The values of
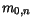 shown in brackets are not taken into account for basic materials. They are used
in the calculation of the relative electron masses in alloy materials.
shown in brackets are not taken into account for basic materials. They are used
in the calculation of the relative electron masses in alloy materials.
Table 3.17:
Parameter values for modeling the effective carrier masses
| Material |
Minimum |
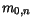 |
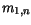 |
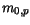 |
 |
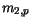 |
| Si |
X |
0.321 |
|
0.009 |
0.55 |
0.6 |
-0.1 |
| Ge |
L (X) |
0.2158 |
(0.42) |
0.0068 |
0.2915 |
0.1 |
|
| GaAs |
 (X) (X) |
0.067 |
(0.471) |
-0.0036 |
0.49 |
|
|
| AlAs |
X ( ) ) |
0.38 |
(0.15) |
-0.0036 |
0.8 |
|
|
| InAs |
 (X) (X) |
0.0237 |
(0.64) |
-0.0027 |
0.41 |
|
|
| InP |
 (X) (X) |
0.077 |
(0.462) |
-0.004 |
0.64 |
|
|
| GaP |
X ( ) ) |
0.5 |
(0.15) |
|
0.6 |
|
|
|
For alloy materials a temperature dependence is introduced first. Then a quadratic
interpolation of the masses is used as a function of the material composition
of an alloy
 .
.
 are bowing parameters summarized in Table 3.18.
are bowing parameters summarized in Table 3.18.
Table 3.18:
Bowing parameter values for modeling the effective carrier masses
| Material |
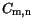 |
 |
Reported Range |
References |
| SiGe |
-0.183 |
-0.096 |
|
|
| AlGaAs |
0.0 |
0.0 |
|
[110,93] |
| InGaAs |
-0.012 |
-0.03 |
0.038-0.044 |
[152,93,153] x=0.53 |
| InAlAs |
0.0 |
0.0 |
0.070-0.083 |
[102,93,111,153] x=0.52 |
| InAsP |
0.0 |
0.0 |
|
|
| GaAsP |
0.0 |
0.0 |
|
|
| InGaP |
0.0 |
0.0 |
0.092-0.118 |
[103,154,155,156] x=0.5 |
|
For materials where the bandgap changes between direct and indirect the
relative electron mass of the lowest band is considered. Such examples are
AlGaAs (Fig. 3.29), InAlAs (Fig. 3.30), InGaP (Fig. 3.31),
and GaAsP. For other materials, such as InGaAs (Fig. 3.32) and InAsP
only the  valley masses are considered. For SiGe a strained bandgap
without X-to-L transition is assumed and only the X-valley masses are used in
the interpolation.
valley masses are considered. For SiGe a strained bandgap
without X-to-L transition is assumed and only the X-valley masses are used in
the interpolation.
Figure 3.29:
Relative masses of electrons and holes in AlGaAs
as a function of the material composition
|
|
Figure 3.30:
Relative masses of electrons and holes in InAlAs
as a function of the material composition
|
|
Figure 3.31:
Relative masses of electrons and holes in InGaP
as a function of the material composition
|
|
Figure 3.32:
Relative masses of electrons and holes in InGaAs
as a function of the material composition
|
|




Next: 3.3.5 Effective Density of
Up: 3.3 Band-Structure
Previous: 3.3.3 Bandgap Narrowing
Vassil Palankovski
2001-02-28
![]() valley is
considered. In the case of materials with indirect bandgaps namely Si, Ge,
AlAs, and GaP the transverse and the longitude electron masses (
valley is
considered. In the case of materials with indirect bandgaps namely Si, Ge,
AlAs, and GaP the transverse and the longitude electron masses (![]() and
and
![]() ) from the X valley (respectively L valley for Ge) are taken into account by
(3.86). For all materials the hole masses are calculated by
(3.87) accounting for the heavy and the light hole masses (
) from the X valley (respectively L valley for Ge) are taken into account by
(3.86). For all materials the hole masses are calculated by
(3.87) accounting for the heavy and the light hole masses (![]() and
and ![]() ) [86].
) [86].
![]() shown in brackets are not taken into account for basic materials. They are used
in the calculation of the relative electron masses in alloy materials.
shown in brackets are not taken into account for basic materials. They are used
in the calculation of the relative electron masses in alloy materials.
![]() .
.
![]() valley masses are considered. For SiGe a strained bandgap
without X-to-L transition is assumed and only the X-valley masses are used in
the interpolation.
valley masses are considered. For SiGe a strained bandgap
without X-to-L transition is assumed and only the X-valley masses are used in
the interpolation.
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CrmAlGaAsx.eps}}](img438.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CrmInAlAsx.eps}}](img439.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CrmInGaPx.eps}}](img440.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/CrmInGaAsx.eps}}](img441.gif)