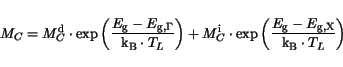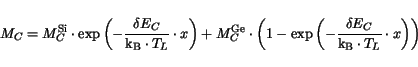Next: 3.4 Carrier Mobility
Up: 3.3 Band-Structure
Previous: 3.3.4 Effective Carrier Mass
The effective density of states (DOS) in the conduction and the valence bands
are expressed by the following theoretical expressions [86]:
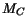 represents the number of equivalent energy minima in the conduction band.
represents the number of equivalent energy minima in the conduction band.
Table 3.19:
Parameter values for energy minima in the DOS model
| Material |
 |
Material |
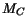 |
| Si |
6 |
InAs |
1 |
| Ge |
4 |
InP |
1 |
| GaAs |
1 |
GaP |
3 |
| AlAs |
3 |
|
|
|
For  an alternative model based on data after
Green [120] is implemented,
which is based on a second order polynomial fit.
an alternative model based on data after
Green [120] is implemented,
which is based on a second order polynomial fit.
Table 3.20:
Parameter values for modeling the effective carrier masses
| Material |
 [cm [cm ] ] |
 [cm [cm ] ] |
 [cm [cm ] ] |
 [cm [cm ] ] |
 [cm [cm ] ] |
 [cm [cm ] ] |
| Si |
-0.14e19 |
1.56e19 |
1.44e19 |
-0.17e19 |
0.93e19 |
2.34e19 |
|
In the model for alloy materials effective carrier masses of the constituents are used
in the expressions (3.91) and (3.92).
In the case of a transition between a direct and an indirect bandgap in III-V
ternary compounds the valley degeneracy factor 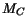 is modeled by an
expression equivalent to the one proposed in [157].
is modeled by an
expression equivalent to the one proposed in [157].
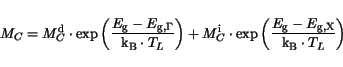 |
(3.94) |
The superscripts  and
and  denote direct and indirect, respectively.
denote direct and indirect, respectively.
In the case of SiGe the splitting of the valley degeneracy due to
strain is modeled accordingly as in [158].
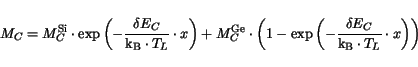 |
(3.95) |
Here,  denotes the energy difference between the valleys shifted
down and up in energy, respectively. It is set equal to 0.6 eV as given in [158].
denotes the energy difference between the valleys shifted
down and up in energy, respectively. It is set equal to 0.6 eV as given in [158].




Next: 3.4 Carrier Mobility
Up: 3.3 Band-Structure
Previous: 3.3.4 Effective Carrier Mass
Vassil Palankovski
2001-02-28


![]() an alternative model based on data after
Green [120] is implemented,
which is based on a second order polynomial fit.
an alternative model based on data after
Green [120] is implemented,
which is based on a second order polynomial fit.
![]() is modeled by an
expression equivalent to the one proposed in [157].
is modeled by an
expression equivalent to the one proposed in [157].