Subsections

• 3.7.5.1 Drift-Diffusion Impact Ionization
• 3.7.5.2 Hydrodynamic Impact Ionization

3.7.5 Impact Ionization

The impact ionization (II) models support both the drift-diffusion (DD) and the hydrodynamic (HD) transport models, therefore, electric field dependent DD II models and carrier temperature dependent HD II models are used in MINIMOS-NT.

3.7.5.1 Drift-Diffusion Impact Ionization

In DD simulation the model from [33] is used to calculate the II generation rates for electrons and holes, respectively. The overall generation rate is the sum of these two generation rates and can be expressed as a negative recombination rate.

$$-R^{\mathrm{II}}=G_{n}^{\mathrm{II}}+G_{p}^{\mathrm{II}}= \a... ...}} \cdot \frac{\left\vert\mathbf{J}_p\right\vert}{\mathrm{q}}.$$ (3.152)

The ionization coefficients $\alpha_{n,\mathrm {bulk}}$ and $\alpha_{p,\mathrm {bulk}}$ are expressed by Chynoweth's law

$$\alpha_{n,\mathrm {bulk}}=\alpha_{n,\mathrm {bulk}}^{\infty}\cdot... ...\mathbf{J}_n \right\vert} {\mathbf{E}\cdot\mathbf{J}_n}\right)^{\beta_n}\right)$$ (3.153)

$$\alpha_{p,\mathrm {bulk}}=\alpha_{p,\mathrm {bulk}}^{\infty}\cdot... ...\mathbf{J}_p \right\vert} {\mathbf{E}\cdot\mathbf{J}_p}\right)^{\beta_p}\right)$$ (3.154)

The default values are summarized in Table 3.38.

Table 3.38: Parameter values for DD impact ionization model

Material	$\alpha_{n,\mathrm {bulk}}$[m$^{-1}$]	$E_{n,\mathrm {bulk}}^{\mathrm {crit}}$[V/m]	$\beta_n$	$\alpha_{p,\mathrm {bulk}}$[m$^{-1}$]	$E_{p,\mathrm {bulk}}^{\mathrm {crit}}$[V/m]	$\beta_p$	Reference
Si	7.03e7	1.231e8	1.0	1.528e8	2.036e8	1.0
Ge	1.55e9	1.560e8	1.0	1e9	1.28e8	1.0	[33]
GaAs	3.5e7	6.85e7	2.0	3.5e7	6.85e7	2.0	[190]
GaP	4.0e7	1.18e8	2.0	4.0e7	1.18e8	2.0	[190]

To account for surface effects, the surface ionization rates $\alpha_{n,\mathrm {surf}}$ and $\alpha_{p,\mathrm {surf}}$ can deviate from the bulk rates. The electron surface ionization rate is calculated in a similar way (analog for holes)

$$\alpha_{n,\mathrm {surf}}=\alpha_{n,\mathrm {surf}}^{\infty}... ...\vert} {\mathbf{E} \cdot\mathbf{J}_n}\right)^{\beta_n}\right).$$ (3.155)

$F(y)$ is given by (3.120) and depending on the surface distance $y$ describes a smooth transition between the surface and bulk generation rates. The parameter $y^\mathrm {ref}$ denotes a critical length. The final surface dependent ionization rate reads

$$\alpha_{n,\mathrm {eff}}=F(y)\cdot \alpha_{n,\mathrm {surf}} + (1-F(y))\cdot\alpha_{n,\mathrm {bulk}}.$$ (3.156)

The effect is considered only for Si and the following values are used:

Table 3.39: Parameter values for surface DD impact ionization model

Material	$\alpha_{n,\mathrm {surf}}$ [m$^{-1}$]	$E_{n,\mathrm {surf}}^{\mathrm {crit}}$ [V/m]	$\alpha_{p,\mathrm {surf}}$ [m$^{-1}$]	$E_{p,\mathrm {surf}}^{\mathrm {crit}}$ [V/m]	$y^\mathrm {ref}$ [nm]
Si	1.03e7	1.50e8	4.0e8	3.0e8	10

3.7.5.2 Hydrodynamic Impact Ionization

In a HD simulation, the carrier temperatures are used as parameters in the hydrodynamic impact ionization model. The implemented equation for the electron generation rate depending on the concentration $n$ and the bandgap energy $E_{\mathrm{g}}$ [191,192] reads (analog for holes)

$$G_n\left(T_n,n\right) = n\cdot A\cdot\left(\left(1+\frac{u}{... ...{2}\cdot\sqrt{u}\cdot \exp\!\left(\frac{-1}{u}\right)\right),$$ (3.157)

$$u = \frac{\mathrm{k_B}\cdot T_n}{E_{\mathrm{g}}}.$$ (3.158)

The prefactor $A$ depends on the carrier and lattice temperatures and the local bandgap

$$A(T_{{\mathrm{L}}},T_n,E_{\mathrm{g}})=\frac{1}{C_1}\!\cdot ... ...\!C_4\!\cdot\! \frac{T_{{\mathrm{L}}}-T_0}{T_0}\right)\right).$$ (3.159)

The variables $T_0$ and $E_0$ correspond to 300 K and $E_{\mathrm{g}}(300 \rm K)$, respectively.

Table 3.40: Parameter values for HD impact ionization model

Material	$C_1$ [s]	$C_2$	$C_3$	$C_4$
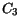Si	9.531e-9	3.823	0.346333	0.0922

The overall generation rate is the sum of the electron and hole generation rates, and is equal to a negative recombination rate

$$R^{\mathrm{II}}=-G_{n}^{\mathrm{II}}-G_{p}^{\mathrm{II}}.$$ (3.160)

Another simple, but very practical model is available for modeling the impact ionization rate in all semiconductors. It reads for electrons

$$G_n\left(T_n,T_{{\mathrm{L}}},n\right) = n\cdot A\cdot\exp\!\left(\frac{-B\cdot E_{\mathrm{g}}}{\mathrm{k_B}\cdot T_n}\right)$$ (3.161)

and, respectively, for holes

$$G_p\left(T_p,T_{{\mathrm{L}}},p\right) = p\cdot A\cdot\exp\!... ...t(\frac{-B\cdot E_{\mathrm{g}}}{\mathrm{k_B}\cdot T_p}\right).$$ (3.162)

The default values recommended for the simple HD II model are summarized in the following table:

Table 3.41: Parameter values for HD impact ionization model

Material	$A$ [s$^{-1}$]	$B$
Si&Ge	1e13	0.92
III-Vs	1e13	1.0

This model has been already successfully applied in simulation of GaAs-based and InP-based HEMTs [193,194]. However, it has not been applied in simulation of III-V HBTs yet.