Prev: 7.1.6 Process Control

7.2 HPCVD of Tungsten

The model for the deposition of tungsten was derived from the reduction of ${\rm WF\hspace*{-0.2ex}_6}$ with hydrogen

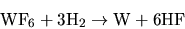$${\rm WF\hspace*{-0.2ex}_6}+ 3 {\rm H_2}\to {\rm W}+ 6 {\rm HF}$$ (7.6)

forming ${\rm HF}$ as by-product. The reaction results in three diffusion equations for the gaseous species ${\rm WF\hspace*{-0.2ex}_6}$, ${\rm H_2}$, and ${\rm HF}$. Tungsten as reaction product is directly deposited as solid at the wafer surface and therefore has not to be considered for the diffusion. It is clear that the reaction chemistry is much more complicated with different adsorbed or chemisorbed intermediates. Furthermore the reduction can be carried out with a combination of hydrogen and silane (${\rm SiH_4}$). For demonstration purposes the chemistry will be restricted to an overall formulation, even if more complex models can be formulated within the Analytical Model Interface.

The derivation of effective species diffusivities in mixtures, which depend on composition, pressure and temperature uses the Chapman-Enskog equation and the characteristic Lennard-Jones length $\sigma$ and energy $\epsilon$ [30][35].

The deposition rate was experimentally found [43] to follow the expression

$$R_H = \frac{c_1 \cdot \exp (-E_A/RT) \cdot [p({\rm WF\hspace*{-0.2ex}_6})] \cdot [p({\rm H_2})]^{1/2}} {1 + c_2 \cdot [p({\rm WF\hspace*{-0.2ex}_6})]}$$ (7.7)

$$c_1 = 4.9 \times 10^{-2} \mathrm{mol \cdot Torr^{-3/2} \cdot cm^{-2} \cdot s^{-1}}$$

$$c_2 = 25 \mathrm{Torr^{-1}}$$

where $c_1$ and $c_2$ are experimentally determined constants, $p({\rm H_2})$ and $p({\rm WF\hspace*{-0.2ex}_6})$ are hydrogen and ${\rm WF\hspace*{-0.2ex}_6}$ partial pressures and $E_A$ is the activation energy which was set to 68.4 kJ/mol [77]. $R$ is the gas constant and $T$ is the temperature. This rate expression is substituted into (7.2) and couples the concentrations of the three gaseous species by the stoichiometry of (7.6). When tungsten is formed at the wafer surface a certain amount of ${\rm WF\hspace*{-0.2ex}_6}$ is consumed from the gas phase, thus reducing the concentration of ${\rm WF\hspace*{-0.2ex}_6}$. The same applies to the hydrogen concentration, differing only in the stoichiometric factor. Simultaneously ${\rm HF}$ is formed and has to be added to the ${\rm HF}$ concentration in the gas phase.

Prev: 7.1.6 Process Control