3.1.1 Basic Semiconductor Equations

Starting from the Maxwell equations the semiconductor equations are derived [251]. The Poisson equation:

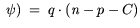$$(\varepsilon  \cdot \psi) = q \cdot ({\it n}_{\mathrm{}}-p-C)$$ (3.1)

and the continuity equations for electrons and holes read:

$${\bf {J}}_n - q \frac{\partial{n}}{ \partial{t}}=q \cdot R$$ (3.2)

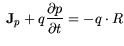$${\bf {J}}_p + q \frac{\partial{p}}{\partial{t}}=-q \cdot R$$ (3.3)

The semiconductor equations (3.1)-(3.3) and the assumptions made have been discussed in a large number of publications [251,268]. $\varepsilon$ represents the permittivity tensor of the semiconductor material mostly approximated by a scalar constant. The potential $\psi$ and the carrier concentrations $n$ and $p$ are to be solved. $C$ gives the concentration of ionized dopands and $R$ the net recombination rate. Before presenting the resulting current relations a few comments shall be made at this point. A very critical issue of the solution of the Boltzmann equation with a finite number of moments are the implicit assumptions made as was stressed for Si by Grasser et al. in [108]. For the actual implementation of energy or hydrodynamic transport models two factors are found relevant for the solution: first the closure relation, i.e., an additional equation to obtain the same number of variables and equations in the finite moment approximation. The second aspect is the influence of the finite number of the moments itself [108]. The impact of both will be discussed with the parameter extraction in Section 3.6.