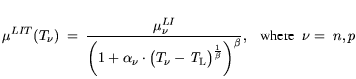Next: 3.2.6 Saturation Velocity
Up: 3.2.5 Carrier Mobility
Previous: 3.2.5.4 High Field Mobility
To clarify the interaction of the model and model parameters a second variant of the high field mobility
is supplied. (3.49) is a variant of the Hänsch model, used e.g. in [178].
The formula reads:
| |
|
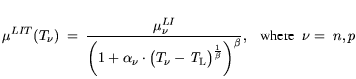 |
(3.46) |
In this approach an additional parameter  is introduced as demonstrated in HEMT simulations in [50].
It was used with constant energy relaxation times and the parameter
is introduced as demonstrated in HEMT simulations in [50].
It was used with constant energy relaxation times and the parameter  allows to match static overshoot effects
obtained by MC simulation in the channel.
This stresses the interaction of the high field parameters obtained within one model.
Section 3.6 shows the acquisition of high field parameters when using the
DD, the HD approach in (3.49), and a HD approach using (3.46) and (3.48) with non-constant energy relaxation times.
Physical effects such as static velocity overshoot can be introduced with the different high field mobility concepts.
Under no circumstances the parameters can be mixed, once calibrated for an particular approach.
Furthermore, each approach supplies a different amount of information. E.g., the
allows to match static overshoot effects
obtained by MC simulation in the channel.
This stresses the interaction of the high field parameters obtained within one model.
Section 3.6 shows the acquisition of high field parameters when using the
DD, the HD approach in (3.49), and a HD approach using (3.46) and (3.48) with non-constant energy relaxation times.
Physical effects such as static velocity overshoot can be introduced with the different high field mobility concepts.
Under no circumstances the parameters can be mixed, once calibrated for an particular approach.
Furthermore, each approach supplies a different amount of information. E.g., the
 bias dependence
of the channel velocities under no circumstances can be fit with the DD approach. However, using
bias dependence
of the channel velocities under no circumstances can be fit with the DD approach. However, using
 and
and  in (3.43)
as fitting parameters, agreement of the channel velocities can be obtained for one bias, as was shown by Bude et al. in [54].
in (3.43)
as fitting parameters, agreement of the channel velocities can be obtained for one bias, as was shown by Bude et al. in [54].



Next: 3.2.6 Saturation Velocity
Up: 3.2.5 Carrier Mobility
Previous: 3.2.5.4 High Field Mobility
Quay
2001-12-21