| Material |
Valley |
v
 [10 [10 cm/s] cm/s] |
A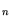 |
v
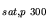 |
A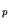 |
References |
| |
|
(for E [kV/cm]) |
|
[10 cm/s] cm/s] |
|
|
| GaAs |
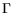 |
0.72 |
0.56 |
0.9 |
0.41 |
[226] |
| |
X |
2.73 |
- |
- |
- |
- |
| AlAs |
X |
0.85 |
0.55 |
0.8 |
0.3 |
[226] |
| |
 |
0.39 |
- |
- |
- |
see Fig. 3.9 |
| InAs |
 |
0.9 |
0.57 |
0.5 |
0.3 |
[226] |
| |
X |
- |
- |
- |
- |
- |
| InP |
|
0.67 |
0.68 |
0.5 |
0.3 |
[226] |
| GaP |
|
0.88 |
0.30 |
0.5 |
0.3 |
[226] |
| GaN |
 |
1.4 |
0.15 |
- |
- |
[17,38] |
| |
|
(for 500) |
|
|
|
|
| AlN |
 |
1.6 |
0.135 |
- |
- |
[17,204] |
| |
|
(for 1000) |
|
|
|
|
| InN |
 |
2.5 |
- |
- |
- |
[17,203] |
| |
|
(for 300) |
|
|
|
|
| Si |
X |
1.0 |
0.26 |
0.704 |
0.63 |
[226] |
|
![]() with the following two parameter model:
with the following two parameter model:
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig-42.eps}](img467.gif)