


Next: 5. Statistical Characterization of
Up: 4. RF-Extraction
Previous: 4.7 Delay Time Extraction
Several compact modeling approaches have been suggested to describe impact ionization within a
device, mostly applied to InAlAs/InGaAs devices. In [75,271,270] a gate
current analysis is given, which suggests the following model: the gate current
 is composed
of a thermionic field emission and an impact ionization component.
is composed
of a thermionic field emission and an impact ionization component.
| |
|
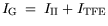 |
(4.31) |
The impact ionization contribution was fitted to the following term:
| |
|
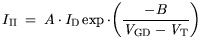 |
(4.32) |
The thermionic contribution was calculated according to the model [270]:
| |
|
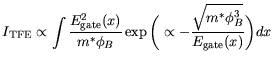 |
(4.33) |
 and
and  are fit parameters and
are fit parameters and
 represents an effective field at the
gate. In [19] another compact model was demonstrated including physical geometries for the
evaluation of gate currents and breakdown voltages in InAlAs/InGaAs HEMTs.
In [20,230] it is mentioned that in a simple macroscopic exponential
model for impact ionization the coefficients obtained from bulk impact ionization experiments
could not be verified fitting gate currents. To understand these discrepancies the information on
the interaction of impact ionization with temperature, the other generation/recombination
mechanisms, the geometry aspect, and the complete information of the energy distribution of the
carriers must be considered in device simulation.
represents an effective field at the
gate. In [19] another compact model was demonstrated including physical geometries for the
evaluation of gate currents and breakdown voltages in InAlAs/InGaAs HEMTs.
In [20,230] it is mentioned that in a simple macroscopic exponential
model for impact ionization the coefficients obtained from bulk impact ionization experiments
could not be verified fitting gate currents. To understand these discrepancies the information on
the interaction of impact ionization with temperature, the other generation/recombination
mechanisms, the geometry aspect, and the complete information of the energy distribution of the
carriers must be considered in device simulation.



Next: 5. Statistical Characterization of
Up: 4. RF-Extraction
Previous: 4.7 Delay Time Extraction
Quay
2001-12-21
![]() is composed
of a thermionic field emission and an impact ionization component.
is composed
of a thermionic field emission and an impact ionization component.