Unterabschnitte

• Ladungsintegration
• Energiemethode
• Feldberechnung
• Randbedingungen
• Teilkapazitäten

2.1 Kapazität

Für den stationären Fall mit linearer Dielektrizitätszahl ist das Verhältnis von Ladung $Q$ und Spannung $U$ zweier voneinander isolierter Leiter konstant und wird als Kapazität $C$ bezeichnet

$$C=\frac{Q}{U}\;.$$ (2.11)

Da die Leiter im Inneren feldfrei sind, ist das Potenzial dort konstant und die Ladung ist ausschließlich auf der Oberfläche der Leiter verteilt.

Ladungsintegration

Die Ladungsverteilung ergibt sich aus der elektrischen Flussdichte  $\mathchoice{\mbox{\boldmath $\displaystyle D$}} {\mbox{\boldmath $\textstyle D$}} {\mbox{\boldmath $\scriptstyle D$}} {\mbox{\boldmath $\scriptscriptstyle D$}}$ gemäß der dritten Maxwell'schen Gleichung (2.3). Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit der Dicke $d$ und lässt $d$ gegen Null gehen, so erhält man die Flächenladungsdichte $\sigma$ als Differenz der Normalkomponenten von $\mathchoice{\mbox{\boldmath $\displaystyle D$}} {\mbox{\boldmath $\textstyle D$}} {\mbox{\boldmath $\scriptstyle D$}} {\mbox{\boldmath $\scriptscriptstyle D$}}$ außerhalb ( $\mathchoice{\mbox{\boldmath $\displaystyle D_o$}} {\mbox{\boldmath $\textstyle... ...mbox{\boldmath $\scriptstyle D_o$}} {\mbox{\boldmath $\scriptscriptstyle D_o$}}$) und innerhalb ( $\mathchoice{\mbox{\boldmath $\displaystyle D_i$}} {\mbox{\boldmath $\textstyle... ...ox{\boldmath $\scriptstyle D_i$}} {\mbox{\boldmath $\scriptscriptstyle D_i$}}=0$) des Leiters

$$\sigma=(\mathchoice{\mbox{\boldmath$\displaystyle D_o$}} {\mbox{\... ... {\mbox{\boldmath$\scriptstyle n$}} {\mbox{\boldmath$\scriptscriptstyle n$}}\;,$$ (2.12)

wobei der Vektor $\mathchoice{\mbox{\boldmath $\displaystyle n$}} {\mbox{\boldmath $\textstyle n$}} {\mbox{\boldmath $\scriptstyle n$}} {\mbox{\boldmath $\scriptscriptstyle n$}}$ normal auf die Leiteroberfläche steht und in Richtung Dielektrikum zeigt. Mittels Ladungsintegration über die Leiteroberfläche $\Gamma _i$

$$Q= \oint_{\Gamma _i} \sigma\,\textrm{d}A = \oint_{\Gamma _i} \mat... ...oldmath$\scriptstyle n$}} {\mbox{\boldmath$\scriptscriptstyle n$}}\,\textrm{d}A$$ (2.13)

kann man die gesamte auf einem Leiter gespeicherte Ladung berechnen. Über (2.11) lässt sich daraus die Kapazität zwischen zwei Leitern ermitteln.^2.1

Energiemethode

Als Alternative zur Ladungsintegration kann die Kapazität auch mit der Energiemethode ermittelt werden. Die in einem Kondensator gespeicherte Energie $W$ lässt sich durch

$$W=\frac{C U^2}2$$ (2.14)

ausdrücken, die natürlich gleich der im elektrischen Feld enthaltenen Energie

$$W=\frac12\int_{\Omega}\!\mathchoice{\mbox{\boldmath$\displaystyle... ...th$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}}\,\textrm{d}\Omega$$ (2.15)

sein muss. Der Integrationsbereich $\Omega$ erstreckt sich über das gesamte Dielektrikum zwischen den Leitern und geht theoretisch bis ins Unendliche. Das elektrische Feld ladungsbalancierter Leiter klingt für Entfernungen, die groß sind gegenüber dem Durchmesser des Gebietes, das die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab. Deshalb ist der größte Teil der Feldenergie in der nächsten Umgebung der Leiter enthalten und der Integrationsbereich kann für praktische Anwendungen entsprechend verkleinert werden, ohne einen großen Fehler bei der Energieberechnung zu machen. In Abb. 2.1 ist grafisch dargestellt wie der Fehler der berechneten Kapazität in einem zweidimensionalen Beispiel von der Größe des Simulationsbereiches abhängig ist.

Abbildung 2.1: Auswirkung der Größe des Simulationsbereiches $w$ auf den Fehler $e$ der berechneten Kapazität in einem zweidimensionalen Beispiel

Abbildung 2.2 vergleicht den zwei- und den dreidimensionalen Fall. Das dreidimensionale Beispiel ist im Querschnitt mit dem zweidimensionalen ident, und die Länge des Leiters entspricht seiner Breite. Man erkennt, dass im zweidimensionalen Fall der Fehler der berechneten Kapazität quadratisch gegen Null geht, während im dreidimensionalen Fall eine Konvergenz mit der dritten Potenz von $w$ beobachtbar ist.

Abbildung 2.2: Vergleich der relativen Fehler, die durch die Einschränkung des Simulationsbereiches entstehen, im zwei- und im dreidimensionalen Fall: Man erkennt, dass im zweidimensionalen Fall der Fehler quadratisch und im dreidimensionalen Fall der Fehler mit der dritten Potenz gegen Null geht.

Feldberechnung

Sowohl die Energiemethode als auch das Verfahren der Ladungsintegration erfordern die numerische Berechnung des elektrischen Feldes. Anzumerken ist, dass bei der Ladungsintegration die Berechnung des Feldes auf der Leiteroberfläche ausreichend ist.

Setzt man (2.10) in (2.3) ein und berücksichtigt, dass in den Isolatoren keine elektrischen Ladungen vorhanden sind ($\rho=0$) erhält man die Euler-Gleichung

$$\mathop\mathrm{div}\left(\makebox{\boldmath$\underline\varepsilon$}\mathop\mathrm{grad}\varphi\right)=0\;.$$ (2.16)

Randbedingungen

Das Gebiet $\Omega$, auf dem Gleichung (2.16) gelöst werden soll wird durch mehrere Flächen berandet (Abb. 2.3).

Abbildung 2.3: Simulationsbereich und Ränder bei der Berechnung des elektrischen Feldes: Die beiden Elektroden $\Omega _1$ und $\Omega _2$ liegen auf konstanten Potenzialen ($V_1$ bzw. $V_2$) und bilden somit Dirichlet-Bedingungen. Der äußere Rand (punktierte Linie) wird durch eine homogene Neumann-Bedingung modelliert.

Die konstanten Potenziale der Leiteroberflächen stellen Dirichlet-Bedingungen dar

$$\forall \mathchoice{\mbox{\boldmath$\displaystyle r$}} {\mbox{\bo... ...ox{\boldmath$\scriptstyle r$}} {\mbox{\boldmath$\scriptscriptstyle r$}})=V_i\;,$$ (2.17)

wobei mit $\Gamma _i$ die Oberfläche des Leiters $i$ bezeichnet wird. Wenn man für die numerische Berechnung das Simulationsgebiet nach außen hin begrenzt, benötigt man auch für $\Gamma _a$ eine Randbedingung, die man sinnvollerweise so wählt, dass die Oberfläche ladungsfrei bleibt, also $\mathchoice{\mbox{\boldmath $\displaystyle D$}} {\mbox{\boldmath $\textstyle D... ...{\mbox{\boldmath $\scriptstyle n$}} {\mbox{\boldmath $\scriptscriptstyle n$}}=0$ gilt, oder durch das Potenzial ausgedrückt:

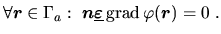$$\forall \mathchoice{\mbox{\boldmath$\displaystyle r$}} {\mbox{\bo... ...mbox{\boldmath$\scriptstyle r$}} {\mbox{\boldmath$\scriptscriptstyle r$}})=0\;.$$ (2.18)

Diese Art von Randbedingung wird homogene Neumann-Bedingung genannt. Oberflächen, auf denen eine fixe elektrische Flächenladungsdichte $\sigma$ eingeprägt ist, lassen sich durch allgemeine Neumann-Bedingungen darstellen:

$$\forall \mathchoice{\mbox{\boldmath$\displaystyle r$}} {\mbox{\bo... ...\boldmath$\scriptstyle r$}} {\mbox{\boldmath$\scriptscriptstyle r$}})=\sigma\;.$$ (2.19)

Eine spezielle Art von Randbedingung wird für den Fall benötigt, wenn sich im Dielektrikum zwischen den beiden Leitern, deren Kapazität berechnet werden soll, ein weiterer leitender Körper befindet, der nicht mittels einer Dirichlet-Bedingung auf ein fixes Potenzial gelegt werden soll. Da hier wie in jedem Leiter $\mathchoice{\mbox{\boldmath $\displaystyle E$}} {\mbox{\boldmath $\textstyle E... ...{\mbox{\boldmath $\scriptstyle E$}} {\mbox{\boldmath $\scriptscriptstyle E$}}=0$ gilt, muss zwar das Potenzial auf der gesamten Oberfläche des Leiters $\Gamma _{\mathrm f}$ gleich groß sein, es wird aber mit einem noch unbekannten Wert $V_{\mathrm f}$ angenommen:

$$\forall \mathchoice{\mbox{\boldmath$\displaystyle r$}} {\mbox{\bo... ...th$\scriptstyle r$}} {\mbox{\boldmath$\scriptscriptstyle r$}})=V_{\mathrm f}\;.$$ (2.20)

Da dieser Leiter über keine elektrischen Anschlüsse verfügt, können Ladungen auf der Oberfläche rein durch Influenz entstehen und müssen in Summe Null ergeben:

$$\oint_{\Gamma _{\mathrm f}}(\makebox{\boldmath$\underline\varepsi... ...th$\scriptstyle n$}} {\mbox{\boldmath$\scriptscriptstyle n$}}\,\textrm{d}A=0\;.$$ (2.21)

Dieser Typ von Randbedingung wird schwebende Randbedingung (Floating Boundary) genannt.

Teilkapazitäten

Bisher wurden zur Kapazitätsberechnung immer nur Zweileitersysteme herangezogen. Geht man jedoch von $n$ Leitern aus, so kann man von jedem Leiter zu jedem anderen eine Kapazität definieren, man erhält also insgesamt $\frac12n(n-1)$ Teilkapazitäten (siehe Beispiel in Abb. 2.4).

Abbildung 2.4: Zehn Teilkapazitäten in einem 5-Leiter Problem

Für eine bestimmte Konfiguration von Potenzialen auf den einzelnen Leitern ($V_1$, $V_2$, ...$V_n$) kann man die Gesamtenergie als Summe der einzelnen Energien in den $\frac12n(n-1)$ Teilkapazitäten anschreiben:

$$W=\sum_{i=1}^{n-1}\sum_{j=i+1}^n\frac{C_{ij}~(V_i-V_j)^2}{2}\;.$$ (2.22)

Man erhält also eine Gleichung mit $\frac12n(n-1)$ Unbekannten. Da für eine Lösung $\frac12n(n-1)$ Gleichungen benötigt werden, berechnet man die Gesamtenergie für $\frac12n(n-1)$ verschiedene Potenzialkonfigurationen der Leiter. Aus dem entstandenem linearen System lassen sich dann die Teilkapazitäten bestimmen.

Fußnoten

... ermitteln.^2.1

Ein ladungsbalanciertes System sei vorausgesetzt.