2. Grundlagen

In diesem Kapitel werden die für die elektrische und thermische Simulation wesentlichen physikalischen Zusammenhänge wiedergegeben und die entsprechenden partiellen Differentialgleichungen und Randbedingungen aufgestellt.

Das elektrische Verhalten eines Systems ist durch die vier Maxwell-Gleichungen

$$\mathop\mathrm{rot}\mathchoice{\mbox{\boldmath$\displaystyle H$}}... ...$}} {\mbox{\boldmath$\scriptstyle H$}} {\mbox{\boldmath$\scriptscriptstyle H$}} =\mathchoice{\mbox{\boldmath$\displaystyle J$}} {\mbox{\boldmath$... ...math$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}}}}{\partial{t}},$$ (2.1)

$$\mathop\mathrm{rot}\mathchoice{\mbox{\boldmath$\displaystyle E$}}... ...$}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}} =-\frac{\partial{\mathchoice{\mbox{\boldmath$\displaystyle B$}} {... ...math$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}}}}{\partial{t}},$$ (2.2)

$$\mathop\mathrm{div}\mathchoice{\mbox{\boldmath$\displaystyle D$}}... ...$}} {\mbox{\boldmath$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}} =\rho,$$ (2.3)

$$\mathop\mathrm{div}\mathchoice{\mbox{\boldmath$\displaystyle B$}}... ...$}} {\mbox{\boldmath$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}} =0,$$ (2.4)

mit den Verknüpfungsbeziehungen

$$\mathchoice{\mbox{\boldmath$\displaystyle D$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}} = \makebox{\boldmath$\underline\varepsilon$}\mathchoice{\mbox{\bo... ...}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}},$$ (2.5)

$$\mathchoice{\mbox{\boldmath$\displaystyle B$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}} = \mu\mathchoice{\mbox{\boldmath$\displaystyle H$}} {\mbox{\boldm... ...}} {\mbox{\boldmath$\scriptstyle H$}} {\mbox{\boldmath$\scriptscriptstyle H$}},$$ (2.6)

$$\mathchoice{\mbox{\boldmath$\displaystyle J$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle J$}} {\mbox{\boldmath$\scriptscriptstyle J$}} = \gamma\mathchoice{\mbox{\boldmath$\displaystyle E$}} {\mbox{\bo... ...}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}},$$ (2.7)

gegeben. Im stationären Fall verschwinden die Zeitableitungen und (2.1), (2.2) vereinfachen sich zu

$$\mathop\mathrm{rot}\mathchoice{\mbox{\boldmath$\displaystyle H$}}... ...$}} {\mbox{\boldmath$\scriptstyle H$}} {\mbox{\boldmath$\scriptscriptstyle H$}} =\mathchoice{\mbox{\boldmath$\displaystyle J$}} {\mbox{\boldmath$... ... {\mbox{\boldmath$\scriptstyle J$}} {\mbox{\boldmath$\scriptscriptstyle J$}}\;,$$ (2.8)

$$\mathop\mathrm{rot}\mathchoice{\mbox{\boldmath$\displaystyle E$}}... ...$}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}} =0\;.$$ (2.9)

Aus (2.9) erkennt man, dass das stationäre elektrostatische Feld wirbelfrei ist. Es lässt sich deshalb durch den (negativen) Gradienten eines skalaren Potenzials ausdrücken

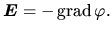$$\mathchoice{\mbox{\boldmath$\displaystyle E$}} {\mbox{\boldmath$\... ...yle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}}=-\mathop\mathrm{grad}\varphi.$$ (2.10)