



Next: 3. Numerische Feldberechnung
Up: 2. Grundlagen
Previous: 2.3 Elektro-quasistatische Analyse
Unterabschnitte
Für eine gekoppelte elektro-thermische Simulation muss zusätzlich zu den
Gleichungen des elektrischen Systems die Wärmeleitungsgleichung gelöst
werden
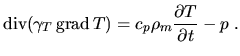 |
(2.43) |
Für den zeitlich unveränderlichen Zustand gilt folgende Vereinfachung:
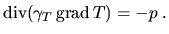 |
(2.44) |
Das Ergebnis dieser Differentialgleichungen ist die Temperatur  .
Die Eigenschaften des Materials gehen durch die thermische
Leitfähigkeit
.
Die Eigenschaften des Materials gehen durch die thermische
Leitfähigkeit  , die spezifische Wärmekapazität
, die spezifische Wärmekapazität  und
die Dichte
und
die Dichte  in die Gleichung ein.
Die Wärmequellendichtefunktion
in die Gleichung ein.
Die Wärmequellendichtefunktion  entspricht der elektrischen
Verlustleistung und berechnet sich aus
entspricht der elektrischen
Verlustleistung und berechnet sich aus
 |
(2.45) |
Diese Gleichung stellt die Kopplung zwischen dem elektrischen und dem
thermischen System dar.
Sowohl die elektrische Leitfähigkeit  als auch die
thermische Leitfähigkeit
als auch die
thermische Leitfähigkeit  vieler
Materialien ist temperaturabhängig; sie werden durch das folgende Modell
angenähert:
vieler
Materialien ist temperaturabhängig; sie werden durch das folgende Modell
angenähert:
 |
(2.46) |
Mit  wird die (elektrische bzw. thermische) Leitfähigkeit bei
einer bestimmten Referenztemperatur
wird die (elektrische bzw. thermische) Leitfähigkeit bei
einer bestimmten Referenztemperatur  (z.B. [300]K) bezeichnet.
Die Faktoren
(z.B. [300]K) bezeichnet.
Die Faktoren  und
und  werden als linearer bzw. quadratischer
Temperaturkoeffizient bezeichnet.
werden als linearer bzw. quadratischer
Temperaturkoeffizient bezeichnet.
Für Metalle gilt das Wiedemann-Franz-Gesetz
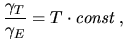 |
(2.47) |
welches besagt, dass das Verhältnis aus thermischer zu elektrischer
Leitfähigkeit proportional zur absoluten Temperatur ist.
Deshalb können die Temperaturkoeffizienten der thermischen Leitfähigkeit
von Metallen ( ,
,  ) näherungsweise aus denen ihrer
elektrischen Leitfähigkeit (
) näherungsweise aus denen ihrer
elektrischen Leitfähigkeit ( ,
,  )
bestimmt werden:
)
bestimmt werden:
Auch die Wärmekapazität  mancher Materialien weist eine Abhängigkeit
von der Temperatur auf.
Sie wird durch die Shomate-Gleichung [73]
mancher Materialien weist eine Abhängigkeit
von der Temperatur auf.
Sie wird durch die Shomate-Gleichung [73]
 |
(2.50) |
modelliert, wobei für  die absolute Temperatur in Kelvin eingesetzt wird.
die absolute Temperatur in Kelvin eingesetzt wird.
Durch die Temperaturabhängigkeiten der elektrischen und thermischen
Leitfähigkeiten bekommt das Gleichungssystem
einen (schwach) nichtlinearen Charakter.
Auch die Massendichte  ist von der Temperatur abhängig.
In dem hier verwendeten Modell bleibt diese Abhängigkeit jedoch
unberücksichtigt, da sonst die Masseerhaltung nicht mehr gegeben
wäre.
Wollte man eine temperaturabhängige Massendichte berücksichtigen,
so wäre es notwendig, zusätzlich noch die thermisch bedingte
Volumsvergrößerung in einem mechanischen System zu berechnen.
ist von der Temperatur abhängig.
In dem hier verwendeten Modell bleibt diese Abhängigkeit jedoch
unberücksichtigt, da sonst die Masseerhaltung nicht mehr gegeben
wäre.
Wollte man eine temperaturabhängige Massendichte berücksichtigen,
so wäre es notwendig, zusätzlich noch die thermisch bedingte
Volumsvergrößerung in einem mechanischen System zu berechnen.
Für den elektrischen Teil des Systems können Randbedingungen angegeben
werden, wie sie bereits bei der Widerstandsberechnung beschrieben wurden.
Für den thermischen Bereich sind folgende Ränder vorgesehen:
Ein (idealer) Kühlkörper, der an einem Teil des Randes  an das Simulationsgebiet angrenzt, mit einer konstanten Temperatur
an das Simulationsgebiet angrenzt, mit einer konstanten Temperatur  ,
wird durch Dirichlet-Bedingungen modelliert:
,
wird durch Dirichlet-Bedingungen modelliert:
 |
(2.51) |
Ein adiabatischer (ideal wärmeisolierender) Rand wird durch eine
homogene Neumann-Bedingung dargestellt:
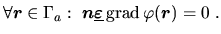 |
(2.52) |
Externe Wärmequellen, die eine konstante Wärmestromdichte  normal
zum Rand einprägen, bedeuten eine inhomogene Neumann-Bedingung:
normal
zum Rand einprägen, bedeuten eine inhomogene Neumann-Bedingung:
 |
(2.53) |
Bei zeitlich veränderlichen Wärmeleitungsproblemen muss zusätzlich
für die Temperatur eine
Anfangsbedingung  vorgegeben werden
vorgegeben werden
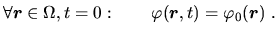 |
(2.54) |




Next: 3. Numerische Feldberechnung
Up: 2. Grundlagen
Previous: 2.3 Elektro-quasistatische Analyse
R. Sabelka: Dreidimensionale Finite Elemente Simulation von Verdrahtungsstrukturen auf Integrierten Schaltungen
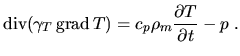
![]() als auch die
thermische Leitfähigkeit
als auch die
thermische Leitfähigkeit ![]() vieler
Materialien ist temperaturabhängig; sie werden durch das folgende Modell
angenähert:
vieler
Materialien ist temperaturabhängig; sie werden durch das folgende Modell
angenähert:



![]() ist von der Temperatur abhängig.
In dem hier verwendeten Modell bleibt diese Abhängigkeit jedoch
unberücksichtigt, da sonst die Masseerhaltung nicht mehr gegeben
wäre.
Wollte man eine temperaturabhängige Massendichte berücksichtigen,
so wäre es notwendig, zusätzlich noch die thermisch bedingte
Volumsvergrößerung in einem mechanischen System zu berechnen.
ist von der Temperatur abhängig.
In dem hier verwendeten Modell bleibt diese Abhängigkeit jedoch
unberücksichtigt, da sonst die Masseerhaltung nicht mehr gegeben
wäre.
Wollte man eine temperaturabhängige Massendichte berücksichtigen,
so wäre es notwendig, zusätzlich noch die thermisch bedingte
Volumsvergrößerung in einem mechanischen System zu berechnen.
![]() an das Simulationsgebiet angrenzt, mit einer konstanten Temperatur
an das Simulationsgebiet angrenzt, mit einer konstanten Temperatur ![]() ,
wird durch Dirichlet-Bedingungen modelliert:
,
wird durch Dirichlet-Bedingungen modelliert:
![]() vorgegeben werden
vorgegeben werden