B.2.1 First-Order Loop

The effect of quantization noise and distortion in a first-order converter circuit is modeled as shown in Fig. B.3. The frequency response of the integrator is $H(s) = 2\pi f_0/s = 1/\tau_0 s$. The integrator distortion and the quantization error are modeled as a signal e(t), which is added to the output.

Figure B.3: First-order sigma-delta converter (noise model)

The unfiltered output Y(s) is then

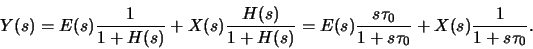$$Y(s) = E(s)\frac{1}{1+H(s)} + X(s)\frac{H(s)}{1+H(s)} = E(s)\frac{s\tau_0}{1+s\tau_0} + X(s)\frac{1}{1+s\tau_0} .$$ (B.2)

Thus, the converter forms a high-pass filter for the quantization error and distortions E(s) and transmits the input signal X(s) up to a frequency $1/2\pi\tau_0$. The power spectral density of the error

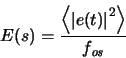$$E(s) = \frac{\left<\left\vert e(t)\right\vert^2\right>}{\ensuremath{f_{\mathit{os}}}\xspace }$$ (B.3)

is constant because of the decorrelation through the randomness of the digital output. Especially, all distortions from the non-linearities of the integrator and the quantizer are spread into noise, which is shifted towards higher frequencies. The in-band noise can be calculated as

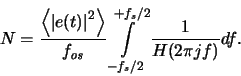$$N = \frac{\left<\left\vert e(t)\right\vert^2\right>}{\ensur... ...suremath{f_{\mathit{s}}}\xspace /2}{\frac{1}{H(2\pi j f)}df} .$$ (B.4)

The resulting SNR is then

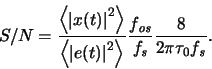$$S/N = \frac{\left<\left\vert x(t)\right\vert^2\right>}{\lef... ...ce } \frac{8}{2\pi\tau_0\ensuremath{f_{\mathit{s}}}\xspace } .$$ (B.5)

The lower limit to $\tau_0$ is set by the oversampling frequency $\tau_0 > 1/\ensuremath{f_{\mathit{os}}}\xspace$.