2.4.2 Lower Bound of the Switching Energy

To determine a lower bound for the switching energy we regard only the intrinsic channel charge of a turned-on transistor (still operating in weak inversion). With

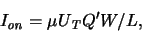$$\ensuremath{I_{\mathit{on}}}\xspace = \mu \ensuremath{U_{\mathit{T}}}\xspace Q' {W}/{L} ,$$ (2.16)

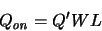$$\ensuremath{Q_{\mathit{on}}}\xspace = Q' W L$$ (2.17)

the channel charge becomes

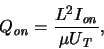$$\ensuremath{Q_{\mathit{on}}}\xspace = \frac{L^2\ensuremath{I... ...thit{on}}}\xspace }{\mu\ensuremath{U_{\mathit{T}}}\xspace } ,$$ (2.18)

where L is the effective channel length and $\mu$ is the effective carrier mobility, and the turn-on current $\ensuremath{I_{\mathit{on}}}\xspace$ for a given supply voltage is adjusted by the channel doping. If we now consider an inverter chain with each output node connected to the two gates of the following stage, and we neglect all other parasitics, then the charge of this node is altered by $4\ensuremath{Q_{\mathit{on}}}\xspace$ during one clock period, so that the switching energy is given by

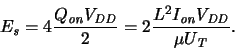$$\ensuremath{E_{\mathit{s}}}\xspace = 4 \frac{\ensuremath{Q_{... ...mathit{DD}}}\xspace }{\mu\ensuremath{U_{\mathit{T}}}\xspace }.$$ (2.19)

This means that the mere device physics does not limit the switching energy, because $\ensuremath{I_{\mathit{on}}}\xspace$ can be chosen almost arbitrarily (disregarding design rules and tunneling effects). However, if we require a node to be charged with at least, say, 10 electrons then (taking $\ensuremath{V_{\mathit{DD,min}}}\xspace$ for $\ensuremath{A_{\mathit{max}}}\xspace > 4$ from Table 2.2) the switching energy is at least 0.13aJ. Another limit comes from the error rate in digital systems subject to thermal noise [75]

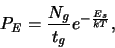$$\ensuremath{P_{\mathit{E}}}\xspace = \frac{\ensuremath{N_{\m... ...space }{e^{-\frac{\ensuremath{E_{\mathit{s}}}\xspace }{kT}}},$$ (2.20)

where is the number of gates and is the gate delay which is larger than the inverter delay

$$\ensuremath{t_{\mathit{d}}}\xspace > 2\frac{\ensuremath{Q_{\... ...pace } = 2\frac{ L^2}{\mu\ensuremath{U_{\mathit{T}}}\xspace }.$$ (2.21)

If we assume, e.g., a deep sub-micron technology with $L=\rm 50nm$ and $\mu \approx \rm 500cm^2/Vs$, and a system with 10⁷ gates requiring less than one error per year, then we get $\ensuremath{t_{\mathit{d}}}\xspace > \rm 4ps$ and $\ensuremath{E_{\mathit{s}}}\xspace > \rm0.25aJ$.

Of course, these values cannot be reached because of the parasitics, most important the gate-drain overlap, junction, and interconnect capacitances, that were not accounted for. When these are included the circuit speed becomes a function of $\ensuremath{I_{\mathit{on}}}\xspace$, making higher currents necessary to keep up the performance and they also add to the switching energy by $C\ensuremath{V_{\mathit{DD}}}\xspace ^2$. Because the parasitics are largely technology dependent a simple general analysis is not possible. However, what can be seen from (2.19) is that the power efficiency scales as 1/L², i.e., the benefit of ULP CMOS increases with down-scaling.

Heisenberg's uncertainty principle does not impose a lower bound on the switching energy but actually another tradeoff between speed and energy [26,45,46]:^2.1

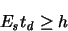$$\ensuremath{E_{\mathit{s}}}\xspace \ensuremath{t_{\mathit{d}}}\xspace \ge \ensuremath{h}\xspace$$ (2.22)

Footnotes

...A0248,R0069,K0134:^2.1

For $\ensuremath{t_{\mathit{d}}}\xspace = \rm4ps$ the minimum energy would be $\rm1.7\cdot10^{-22}J$.