2.8 Single Electron Transistor

    Adding to the double tunnel junction a gate electrode V_g which is capacitively coupled to the island, and with which the current flow can be controlled, a so-called SET transistor is obtained (see Fig. 2.12).

  

Figure 2.12: SET transistor.

The first experimental SET transistors were fabricated by T. Fulton and G. Dolan [35] and L. Kuzmin and K. Likharev [71] already in 1987. The effect of the gate electrode is that the   background charge q₀ can be changed at will, because the gate additionally polarizes the island, so that the island charge becomes
$$\begin{gather}q=-ne+q_0+C_g(V_g-V_2). \end{gather}$$
The formulas derived in Section 2.7 for the double junction can be modified to describe the SET transistor. Substituting $q_0\rightarrow q_0+C_g(V_g-V_2)$ in (2.33), the new voltages across the junctions are
 $$\begin{gather} V_1=\frac{(C_2+C_g)V_b-C_gV_g+ne-q_0}{C_{\Sigma}}, \quad V_2=\frac{C_1V_b+C_gV_g-ne+q_0}{C_{\Sigma}}, \end{gather}$$
with $C_{\Sigma}=C_1+C_2+C_g$. The electrostatic energy has to include also the energy stored in the gate capacitor, and the work done by the gate voltage has to be accounted for in the free energy. The change in  free energy after a tunnel event in junctions one and two becomes
$$\begin{gather}\Delta F_1^{\pm}= \frac{e}{C_{\Sigma}} \left(\frac{e}{2}\pm ((C_2... ...e}{C_{\Sigma}} \left(\frac{e}{2}\pm (V_bC_1+V_gC_g-ne+q_0)\right). \end{gather}$$
At zero temperature only transitions with a negative change in free energy, $\Delta F_1<0$ or $\Delta F_2<0$, are allowed. These conditions may be used to generate a stability plot in the V_b-V_g plane, as shown in Fig. 2.13.

  

Figure 2.13: Stability plot for the SET transistor. The shaded regions are stable regions.

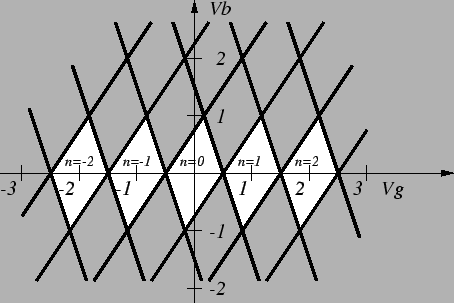The shaded regions correspond to stable regions with an integer number of excess electrons on the island, neglecting any non-zero   background charge. If the gate voltage is increased, and the bias voltage is kept constant below the Coulomb blockade, $V_b<e/C_{\Sigma}$, which is equivalent to a cut through the stable regions in the stability plot, parallel to the x-axis, the current will oscillate with a period of e/C_g. As opposed to the  Coulomb oscillations in a single junction, which were explained in the introduction1, where the periodicity in time of discrete tunnel events is observed, these are Coulomb oscillations which have a periodicity in an applied voltage, where regions of suppressed tunneling and    space correlated tunneling alternate. Fig. 2.14 shows the qualitative shape of the current oscillations.

  

Figure 2.14: Coulomb oscillations in a SET transistor.

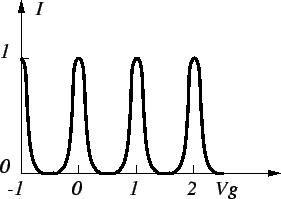Increasing the bias voltage will increase the line-width of the oscillations, because the regions where current is allowed to flow grow at the expense of the remaining Coulomb blockade region. Thermal broadening at higher temperatures or a discrete energy spectrum change the form of the oscillations considerably. Coulomb oscillations have been theoretically investigated by C. Beenakker [15].