2.9 Co Tunneling

  In Section 2.4.2, the tunnel rate was derived from first order perturbation theory. However, in the Coulomb blockade regime, where the first order tunnel rate is very low, or at zero temperature even zero, higher order processes may become important. In the case of the double tunnel junction, a second order process is also possible for bias voltages below the Coulomb blockade, because the change in free energy for a process with tunneling in both junctions is negative even though the energy differences for independent tunneling at either junction are positive. Since one elementary charge is transported over the whole bias voltage drop, for a second order tunnel event in field direction, the change in free energy is -eV_b. In multiple tunnel junction circuits higher order co-tunneling is possible. Generally a circuit consisting of N junctions will show co-tunneling up to the Nth order. Second order co-tunneling looks like a simultaneous tunneling of two electrons through two junctions, which suggests the term co-tunneling. From another point of view this process is a quantum tunneling through a barrier built by two junctions and the island. Since the island may be quite large the resulting structure of tunnel junction - island - tunnel junction, compared to a single junction, is macroscopic, and hence the process is also called    macroscopic quantum tunneling of charge (q-MQT).

Fig. 2.15 shows the energy diagram of the   inelastic and   elastic co-tunneling.

  

Figure 2.15: Energy diagram for co-tunneling. Two distinct forms of co-tunneling, elastic and inelastic co-tunneling, are observable.

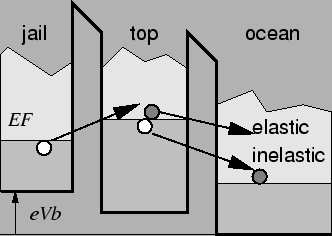Electrons are allowed to tunnel via an  intermediate virtual state where first order tunneling would be suppressed. Suppose an electron cannot tunnel directly from jail to ocean. Also tunneling from jail to top is impossible because of missing energy. Nevertheless, an electron will escape to ocean via an intermediate virtual state, where two simultaneous tunnel events have an overall negative change in free energy. One could picture this process in the following simplified way. An electron starting at jail overcomes the energy difference to top, violating the energy conservation for a very short time allowed by Heisenberg's uncertainty principle. If a different electron from top tunnels in the same very short time to ocean, then overall an electron escaped from jail to ocean. This process is called inelastic co-tunneling, because it produces an electron-hole excitation in the island which is eventually dissipated through carrier-carrier interactions. A second process, the elastic co-tunneling corresponds to the same electron tunneling into and out of a virtual state. An electron tunnels through either one junction, travels through the island, and finally tunnels out of the island through the other junction. The phase of the electron is preserved which makes elastic co-tunneling a coherent process. Elastic co-tunneling strongly depends on the internal structure of the island. Usually inelastic co-tunneling is dominant in comparison to elastic co-tunneling except at very small bias voltages and temperatures or very low energy  state densities in the quantum dot [10] [11]. Inelastic co-tunneling in small normal-metal tunnel junctions, as opposed to superconducting tunnel junctions, was first experimentally observed by L. Geerligs et al. [40], in a silicon quantum dot by H. Matsuoka and S. Kimura [84], and elastic co-tunneling by A. Hanna et al. [50]. Co-tunneling is a major source of errors in SET devices. Especially in SET logic devices that rely on the presence or absence of a single or few number of electrons, co-tunneling is an important issue to consider.

Using   Fermi's golden rule (Appendix E) [30], the  second order co-tunneling rate may be written as [11]
$$\begin{gather}\Gamma^{(2)}=\frac{2\pi}{\hbar}\vert T_1\vert^2\vert T_2\vert^2\le... ...frac{1}{\Delta F_1}+ \frac{1}{\Delta F_2}\right)^2\delta(E_i-E_f), \end{gather}$$
where $\Delta F_x$ is the difference in free energy for tunneling through the xth barrier. The two terms, $1/\Delta F_1$ and $1/\Delta F_2$, represent the fact, that the process could start either with a tunneling in junction one or two. Summing over all possible initial and final states, the total  tunnel rate for the general case of Nth-order co-tunneling is given by [10] [12] [43]
  $$\begin{gather} \Gamma^{(N)}=\frac{2\pi}{\hbar}\left(\prod_{i=1}^N\frac{\hbar}{2\... ... \varepsilon_k=\Delta F_k+\sum_{l=1}^k (\omega_{2l-1}+\omega_{2l}), \end{gather}$$
where the $\omega_x$ are the intermediate energy levels electrons tunnel to and from, and $\text{perm}(k_1,\ldots,k_N)$ denotes all permutations of the numbers $k_1,\ldots,k_N$. An Nth-order co-tunneling event starts at energy level F₀ and passes through levels $F_1,\ldots,F_{N-1},F_N$, as shown in Fig. 2.16. $\Delta F_x$ denotes the difference to the initial level, $\Delta F_x = F_x-F_0$. The quantum mechanical amplitudes of all co-tunneling sequences with the same initial and final states are added coherently to give the total rate (2.44). For different sequences with the same initial and final level, the intermediate levels F_x need not be necessarily the same. It is not possible to solve (2.44) in the general case. Second order co-tunneling at zero temperature is one of the special cases where an analytic solution exists (see Appendix F).
$$\begin{gather}\Gamma^{(2)}\arrowvert_{T=0}=\frac{\hbar V_b}{2\pi e^3R_{T1}R_{T2}... ...ln \left\vert 1+\frac{eV_b}{\Delta F_i}\right\vert\right)-2\right] \end{gather}$$
An approximation introduced by H. Jensen and J. Martinis [56] for (2.44) is to assume that the free energy difference $\Delta F_N$ is, on the average, equally divided over the electron-hole excitation energies. Thus, $\omega_x=-\Delta F_N/2N$, and (2.46) becomes
$$\begin{gather}\varepsilon_k=\Delta F_k-\frac{k}{N}\Delta F_N. \end{gather}$$
The co-tunneling rate may then be analytically calculated as
 $$\begin{align} \Gamma^{(N)}=&\frac{2\pi}{\hbar} \left(\prod_{i=1}^N\frac{\hbar}{... ..._BT}}-1} \prod_{i=1}^{N-1}\left((2\pi k_BTi)^2+\Delta F_N^2\right). \end{align}$$
The result of the perturbative calculation (2.44)   diverges if there are states with energies F_k in the window $F_N\leq F_k\leq F_0$. A consequence of this is the divergence of (2.49) for $\Delta F_k=(k/N)\Delta F_N$. L. Fonseca et al. [32] suggested to move all levels F_k that fall in this window a distance k_BT over the nearest border in order to avoid all divergences. Another possibility to regularize the singularities is to take the  finite lifetime of island states into account [69] or to partially re-sum the infinite perturbation expansion [72]. A theory for    inelastic co-tunneling through a quantum dot in the regime of strong tunneling, where one or both contacts are close to perfect transmission was developed in [36].

  

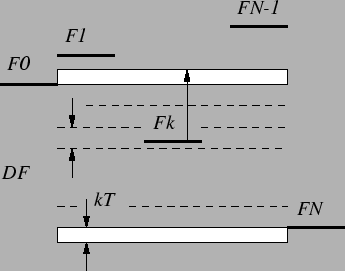
Figure 2.16: Energy levels of an Nth-order co-tunneling event. The dashed lines give the points where the tunnel rate approximation (2.49) diverges. To circumvent the singularities, energy levels falling in the range [F₀,F_N] are moved to the closer border. The buffer zones k_BT have to be added to prevent a second divergence in the case of F₀=F_N.