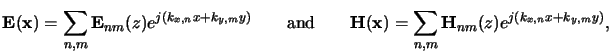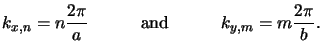6.2 Lateral Discretization of the Maxwell Equations

In this section we discuss the lateral discretization of the Maxwell equations. For a summary confer also the first item of the enumeration listed on page .

Due to the assumption of a periodic simulation domain the inhomogeneous permittivity $\varepsilon$(x) as well as its reciprocal $\chi$(x) = $\varepsilon^{-1}_{}$(x) can be represented by Fourier series

 

$$\varepsilon(\mathbf{x}) = \sum_{n,m} \varepsilon_{nm}(z) e^{j2\pi... ...ext{and}\qquad \chi(\mathbf{x}) = \sum_{n,m} \chi_{nm}(z) e^{j2\pi(nx/a+my/b)},$$ (6.10)

whereby the periods a and b in x- and y-direction, respectively, are the lateral extensions of the simulation domain. Furthermore the incident field is periodic due to the periodic property of the photomask. Because of the periodicity of both the excitation and the permittivity also the disturbance inside the simulation domain must be periodic (cf. (6.10)). Hence, we can expand the electric as well as the magnetic phasor, E(x) and H(x), respectively, into Fourier series, i.e.,

 

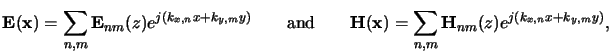$$\mathbf{E}(\mathbf{x}) = \sum_{n,m}\mathbf{E}_{nm}(z) e^{j(k_{x,n... ...\mathbf{H}(\mathbf{x}) = \sum_{n,m}\mathbf{H}_{nm}(z) e^{j(k_{x,n}x+k_{y,m}y)},$$ (6.11)

with discrete lateral wavevector components

 

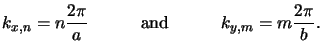$$k_{x,n}=n\frac{2\pi}{a} \quad\qquad\text{and}\quad\qquad k_{y,m}=m\frac{2\pi}{b}.$$ (6.12)

These expansions are similar to those introduced for the vector-valued extension of Fourier optics in Section 4.1.5 and the analysis of the stratified medium in Appendix C. The fundamental difference to (4.55) and (C.1) lies in the fact that we cannot consider planar waves traveling through a homogeneous medium. In the simple homogeneous case the vertical dependence is known and is described by the exponential function with real or complex argument depending on whether the medium is ideally dielectric or absorptive, respectively. In case of inhomogeneous materials the eigenfunctions of the PDE are not known and can, in general, only be determined numerically.

Insertion of the material expansions (6.11) and the field expansions (6.12) into the first and second Maxwell equations (6.5) transforms the PDE valid in the spatial domain to a system of ODEs valid inside the Fourier domain.