



Next: 3.2.4 Specific heat
Up: 3.2 Lattice and Thermal
Previous: 3.2.2 Mass Density
The temperature dependence of
 of the basic materials and insulators is
modeled by a simple power law
of the basic materials and insulators is
modeled by a simple power law
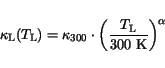 |
(3.55) |
where  is the value for the thermal conductivity at 300 K. This
approximation is in good agreement with experimental data
[105,106,107,108], as presented in Fig. 3.1 and Fig. 3.2
where comparisons in the temperature range from 300 K to 800 K. The parameter
values used are summarized in Table 3.5.
is the value for the thermal conductivity at 300 K. This
approximation is in good agreement with experimental data
[105,106,107,108], as presented in Fig. 3.1 and Fig. 3.2
where comparisons in the temperature range from 300 K to 800 K. The parameter
values used are summarized in Table 3.5.
Table 3.5:
Parameter values for thermal conductivity
| Material |
 [W/K m] [W/K m] |
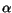 |
Reported  [W/K m] [W/K m] |
References |
| Si |
148 |
-1.3 |
150 |
[85,86] |
| Ge |
60 |
-1.25 |
60 |
[85,86] |
| GaAs |
46 |
-1.25 |
45.5-46 |
[108,92,85,86] |
| AlAs |
80 |
-1.37 |
80 |
[108] |
| InAs |
27.3 |
-1.1 |
27.3-48 |
[108,92] |
| InP |
68 |
-1.4 |
68 |
[108,92] |
| GaP |
77 |
-1.4 |
77 |
[108,92] |
SiO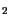 |
1.38 |
0.33 |
1.4 |
[85,86] |
Si N N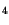 |
18.5 |
0.33 |
15-27 |
[98] |
|
In the case of alloy materials
 ,
,
 varies between
the values of the basic materials (A and B). A harmonic mean is used to model
varies between
the values of the basic materials (A and B). A harmonic mean is used to model
 . An additional bowing factor
. An additional bowing factor  is introduced in order
to account for the drastic reduction of the thermal conductivity with the
increase of material composition
is introduced in order
to account for the drastic reduction of the thermal conductivity with the
increase of material composition  . The exponent
. The exponent 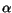 is linearly
interpolated because of lack of experimental data at temperatures other than
300 K.
is linearly
interpolated because of lack of experimental data at temperatures other than
300 K.
The parameter values used are summarized in Table 3.6.
Table 3.6:
Parameter values for thermal conductivity bowing factor
| Material |
 [W/K m] [W/K m] |
| SiGe |
2.8 |
| AlGaAs |
3.3 |
| InGaAs |
1.4 |
| InAlAs |
3.3 |
| InAsP |
3.3 |
| GaAsP |
1.4 |
| InGaP |
1.4 |
|
In Fig. 3.3 and Fig. 3.4 comparisons between data from
[106,107,108,109,110,111] and the results obtained with our
model are shown for the thermal conductivity in alloy materials at 300 K.
Figure 3.1:
Temperature dependence of the thermal conductivity:
Comparison between experimental data and the model for Si, Ge, and GaP
|
|
Figure 3.2:
Temperature dependence of the thermal conductivity:
Comparison between experimental data and the model for InP, GaAs, and InAs
|
|
Figure 3.3:
Material composition dependence of the thermal conductivity:
Comparison between experimental data and the model for SiGe and InGaAs
|
|
Figure 3.4:
Material composition dependence of the thermal conductivity:
Comparison between experimental data and the model for InAsP and AlGaAs
|
|




Next: 3.2.4 Specific heat
Up: 3.2 Lattice and Thermal
Previous: 3.2.2 Mass Density
Vassil Palankovski
2001-02-28
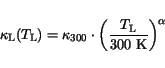
![]() ,
,
![]() varies between
the values of the basic materials (A and B). A harmonic mean is used to model
varies between
the values of the basic materials (A and B). A harmonic mean is used to model
![]() . An additional bowing factor
. An additional bowing factor ![]() is introduced in order
to account for the drastic reduction of the thermal conductivity with the
increase of material composition
is introduced in order
to account for the drastic reduction of the thermal conductivity with the
increase of material composition ![]() . The exponent
. The exponent ![]() is linearly
interpolated because of lack of experimental data at temperatures other than
300 K.
is linearly
interpolated because of lack of experimental data at temperatures other than
300 K.
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/Ctc1.eps}}](img297.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/Ctc2.eps}}](img298.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/Ctcx1.eps}}](img299.gif)
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/Ctcx2.eps}}](img300.gif)