


Next: 3.2.9 Direct Generation/Recombination
Up: 3.2 Material Models
Previous: 3.2.7 Energy Relaxation Times
Although HEMTs are considered unipolar devices, phenomena such as
frequency dispersion, gate currents, and electroluminescence
experiments give a strong hint of the influence of holes, in particular, their
generation and recombination in these devices.
The generation/recombination rates are modeled according to the well known
formulae:
| |
|
 and: and: |
(3.52) |
using:
| |
|
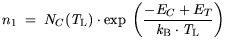 |
(3.53) |
and:
| |
|
 |
(3.54) |
The thermal recombination velocity is defined as:
| |
|
 |
(3.55) |
Corrections are applied to the lifetimes at
 = 300 K according to:
= 300 K according to:
| |
|
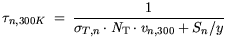 |
(3.56) |
and:
| |
|
 |
(3.57) |
where  and
and  are the surface recombination velocities to correct the influence of
surface. y represents the distance to the surface. The temperature dependence is modeled according to:
are the surface recombination velocities to correct the influence of
surface. y represents the distance to the surface. The temperature dependence is modeled according to:
| |
|
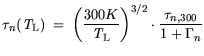 |
(3.58) |
and:
| |
|
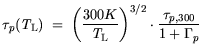 |
(3.59) |
where
 is the field enhancement factor only
relevant for materials with an indirect band gap. Thus, the trap
assisted band to band tunneling (TBB) is neglected for direct
band gap materials. The parameters for the SRH recombination
model are summarized in Table 3.23. The exact traps energies
have to be checked with analysis of the growth process given in
the references. In this work, for AlGaAs midgap traps of
is the field enhancement factor only
relevant for materials with an indirect band gap. Thus, the trap
assisted band to band tunneling (TBB) is neglected for direct
band gap materials. The parameters for the SRH recombination
model are summarized in Table 3.23. The exact traps energies
have to be checked with analysis of the growth process given in
the references. In this work, for AlGaAs midgap traps of 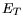 =
0.8 eV were used. For InGaAs
=
0.8 eV were used. For InGaAs 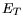 = 0.3 eV was typically assumed.
The lifetimes obtained by (3.59)-(3.62), i.e. the
product of
= 0.3 eV was typically assumed.
The lifetimes obtained by (3.59)-(3.62), i.e. the
product of 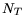 and
and
 can be controlled by
measurements of the minority lifetime in material of the same
growth type, e.g. given in [7]. In
Al
can be controlled by
measurements of the minority lifetime in material of the same
growth type, e.g. given in [7]. In
Al Ga
Ga As, though a direct semiconductor for x
As, though a direct semiconductor for x  0.45, the lifetime is dominated by SRH recombination. For the
surface recombination velocity typical values are given.
0.45, the lifetime is dominated by SRH recombination. For the
surface recombination velocity typical values are given.
Table 3.23:
Relative Shockley-Read-Hall recombination model parameter
values.
| Material |
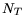 |
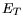 |
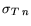 |
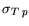 |
S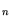 |
S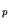 |
References |
| |
[cm ] ] |
[eV] |
[cm ] ] |
[cm ] ] |
[cm/s] |
[cm/s] |
|
| GaAs |
1e14 |
0.2-0.8 |
1e-16 (MBE) |
- |
- |
0 |
[215] |
| InP |
1e13 |
0.1-0.5 |
 1.7e-13 1.7e-13 |
- |
- |
- |
[143,214] |
| Si |
1e13 |
0 |
1e-15 |
1e-15 |
100 |
1e2-1e5 |
[146,251] |
Al Ga Ga As As |
1e15-1e16 |
0.2-0.8 |
5e-14 |
5e-15 |
0 |
0 |
[216] |
In Ga Ga As As |
 1e15 1e15 |
0.17-0.5 |
1e-15 |
- |
0 |
0 |
[41] |
|



Next: 3.2.9 Direct Generation/Recombination
Up: 3.2 Material Models
Previous: 3.2.7 Energy Relaxation Times
Quay
2001-12-21
 and:
and: