3.1.6 Clock Frequency

In a synchronous digital system (cf. Section A.3.1) the minimum cycle time depends on the clocking scheme, the average delay of a logic block (including storage elements), and on the required time margin to allow for latch setup and clocking skew. Average delay times can be used rather than maximum delays because the gates in a critical path can usually be optimized to not exceed this value [5]. Assuming flip-flops as storage elements and single-phase clock ^3.1 the cycle time T_c can be expressed as

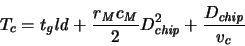$$T_c = \ensuremath{t_{\mathit{g}}}\xspace \ensuremath{{\math... ...{\mathit{chip}}}\xspace }{\ensuremath{v_{\mathit{c}}}\xspace }$$ (3.11)

where is the logic depth and is the chip diameter. The term $\ensuremath{{\mathit{ld}}}\xspace \ensuremath{t_{\mathit{g}}}\xspace$ accounts for the delays of the gates and storage elements (including setup time and skew), and the second term represents an upper bound for the RC-delay of global interconnections (usually on a higher metal layer) which cannot be reduced by inserting buffers. The last term accounts for limitations from the speed of light or electromagnetic waves on transmission lines. Unless very large chips with low-resistance interconnections are considered this term is usually negligible. The maximum clock frequency is then the reciprocal of the cycle time:

$$\ensuremath{f_{\mathit{c,max}}}\xspace = \left[\ensuremath{... ...p}}}\xspace }{\ensuremath{v_{\mathit{c}}}\xspace }\right]^{-1}$$ (3.12)

Footnotes

... clock^3.1

(3.11) applies also to single-latch two-phase systems. Further clocking schemes are described, e.g., in [5].