2.1.4 Das Banddiagramm (Bändermodell)




Next: 2.1.5 Die Zustandsdichte
Up: 2.1 Quantenmechanische Grundlagen
Previous: 2.1.3 Die effektive Masse
In Bauelementen sind zusätzlich zum Kristallpotential
 eingebaute
und angelegte Makropotentiale
eingebaute
und angelegte Makropotentiale  vorhanden.
Das eingebaute Potential ist durch inhomogene Dotierung bedingt, das angelegte
Potential ist auf die im jeweiligen Arbeitspunkt anliegende Spannung
zurückzuführen.
Das Verhalten eines einzelnen Kristallelektrons im Makropotential
vorhanden.
Das eingebaute Potential ist durch inhomogene Dotierung bedingt, das angelegte
Potential ist auf die im jeweiligen Arbeitspunkt anliegende Spannung
zurückzuführen.
Das Verhalten eines einzelnen Kristallelektrons im Makropotential  , das
dem Kristallpotential
, das
dem Kristallpotential  überlagert wird, ohne es zu beeinflussen,
kann von der Schrödingergleichung (2.1) beschrieben werden
(
überlagert wird, ohne es zu beeinflussen,
kann von der Schrödingergleichung (2.1) beschrieben werden
( ).
Nimmt man an, daß das von
).
Nimmt man an, daß das von  bedingte elektrische Feld zu schwach ist,
um Übergänge von einem Band in ein anderes zu induzieren,
läßt sich Gl. (2.1) (
bedingte elektrische Feld zu schwach ist,
um Übergänge von einem Band in ein anderes zu induzieren,
läßt sich Gl. (2.1) ( ) umformen [121]:
) umformen [121]:

Der neue, äquivalente Hamiltonoperator in Gl. (2.20) enthält
die potentielle Energie  des periodischen Kristallpotentials explizit
nicht mehr.
Ersetzt man die Bandstruktur
des periodischen Kristallpotentials explizit
nicht mehr.
Ersetzt man die Bandstruktur  in Gl. (2.20) durch
Gl. (2.18), ergibt sich die Schrödingergleichung für ein freies
Teilchen mit der effektiven Masse
in Gl. (2.20) durch
Gl. (2.18), ergibt sich die Schrödingergleichung für ein freies
Teilchen mit der effektiven Masse  im Feld des Potentials
im Feld des Potentials
 .
Das periodische Potential wird in die Eigenschaften des Wellenpakets
inkorporiert.
Das Wellenpaket verhält sich im elektrischen Feld wie ein sonst freies
Teilchen mit der durch
.
Das periodische Potential wird in die Eigenschaften des Wellenpakets
inkorporiert.
Das Wellenpaket verhält sich im elektrischen Feld wie ein sonst freies
Teilchen mit der durch  gegebenen Dispersionsbeziehung zwischen
Energie und Wellenvektor.
Allerdings ist nicht zu vergessen, daß die Gültigkeit der
effektive-Masse-Näherung in Anwesenheit von Makropotentialen
streng genommen auf Elektronen in unmittelbarer
Nähe der Bandränder in schwachen, langsam veränderlichen Feldern
beschränkt bleibt [120], [121].
gegebenen Dispersionsbeziehung zwischen
Energie und Wellenvektor.
Allerdings ist nicht zu vergessen, daß die Gültigkeit der
effektive-Masse-Näherung in Anwesenheit von Makropotentialen
streng genommen auf Elektronen in unmittelbarer
Nähe der Bandränder in schwachen, langsam veränderlichen Feldern
beschränkt bleibt [120], [121].
Gl. (2.20) erlaubt nach dem Korrespondenzprinzip die Einführung
einer klassischen Hamiltonfunktion:

 stellt die Gesamtenergie
stellt die Gesamtenergie  eines
im gestörten Halbleiter als klassisches Teilchen betrachteten
Elektrons als Funktion des
Wellenvektors
eines
im gestörten Halbleiter als klassisches Teilchen betrachteten
Elektrons als Funktion des
Wellenvektors  (bzw. Impulses
(bzw. Impulses  )
und des Ortes
)
und des Ortes  dar.
Die Gesamtenergie setzt sich aus der Bandenergie
dar.
Die Gesamtenergie setzt sich aus der Bandenergie
 und der potentiellen Energie
und der potentiellen Energie  der externen
Störung zusammen.
Die Bandenergie
der externen
Störung zusammen.
Die Bandenergie  ist die Energie eines Bloch-Elektrons
im ungestörten Kristallgitter ohne eingebaute und angelegte Felder.
Gl. (2.21) impliziert die Gültigkeit der Bandstruktur des ungestörten
Kristalls auch bei Anwesenheit von Makropotentialen
ist die Energie eines Bloch-Elektrons
im ungestörten Kristallgitter ohne eingebaute und angelegte Felder.
Gl. (2.21) impliziert die Gültigkeit der Bandstruktur des ungestörten
Kristalls auch bei Anwesenheit von Makropotentialen  .
Setzt man Gl. (2.18) mit
.
Setzt man Gl. (2.18) mit  in Gl. (2.21) ein,
ergibt sich für Elektronen im Leitungsband:
in Gl. (2.21) ein,
ergibt sich für Elektronen im Leitungsband:
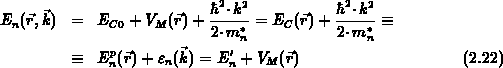
Die beiden ersten Ausdrücke der rechten Seite von Gl. (2.22) stellen
die potentielle Energie dar.
 ist die potentielle Energie des Elektrons im
ungestörten Kristall.
Der letzte Term ist die
ist die potentielle Energie des Elektrons im
ungestörten Kristall.
Der letzte Term ist die  Relation
für parabolische, isotrope Bänder in der Nähe des Bandminimums.
Er entspricht der kinetischen Energie eines freien Teilchens mit der
effektiven Masse
Relation
für parabolische, isotrope Bänder in der Nähe des Bandminimums.
Er entspricht der kinetischen Energie eines freien Teilchens mit der
effektiven Masse  .
.
 ist die Leitungsbandkante.
Sie stellt die gesamte potentielle Energie dar.
ist die Leitungsbandkante.
Sie stellt die gesamte potentielle Energie dar.
 ist aufgrund eingebauter und angelegter Potentiale ortsabhängig.
Die Gesamtenergie eines Elektrons im Leitungsband setzt sich aus der
potentiellen Energie
ist aufgrund eingebauter und angelegter Potentiale ortsabhängig.
Die Gesamtenergie eines Elektrons im Leitungsband setzt sich aus der
potentiellen Energie  und der kinetischen Energie
und der kinetischen Energie  zusammen.
(Anmerkung: Obwohl in dieser Arbeit nur Standardbänder betrachtet
werden, wird
zusammen.
(Anmerkung: Obwohl in dieser Arbeit nur Standardbänder betrachtet
werden, wird  allgemein als Funktion des Wellenvektors
allgemein als Funktion des Wellenvektors  und
nicht als Funktion seines Betrages
und
nicht als Funktion seines Betrages  geschrieben).
geschrieben).
Bisher wurde das Elektron unter dem Einfluß des Kristallpotentials und
eingebauter und angelegter Makropotentiale betrachtet.
Streuprozesse sind in die bisherige Betrachtung nicht eingegangen.
Weil die Bewegung des Elektrons ohne Streuprozesse erfolgt, bleibt die
Gesamtenergie konstant.
Die Forderung der verschwindenden zeitlichen Änderung
von  ergibt [120]:
ergibt [120]:

Daraus folgt in Übereinstimmung mit Gl. (2.9), (2.10):

In der semiklassichen Näherung wird das Elektronenwellenpaket als
klassisches Teilchen
behandelt, das in eingebauten und
angelegten Feldern den Newton'schen Bewegungsgesetzen gehorcht.
Das Kristallpotential
tritt explizit nicht in Erscheinung. Es ist implizit in der effektiven
Masse und in der Bandstruktur enthalten.
Die Trägerstreuung
muß quantenmechanisch behandelt werden, weil Kollisionen teilweise
schnell veränderliche Potentiale implizieren.
Für Löcher erhält man zu (2.22) analoge Ausdrücke:

Das Banddiagramm  stellt die energetischen Verhältnisse für den
Grenzfall des ruhenden Elektrons (oder Lochs) (
stellt die energetischen Verhältnisse für den
Grenzfall des ruhenden Elektrons (oder Lochs) ( ) dar.
Während die Bandstruktur
) dar.
Während die Bandstruktur  einen mikroskopischen
Zusammenhang wiedergibt, ist das Banddiagramm
einen mikroskopischen
Zusammenhang wiedergibt, ist das Banddiagramm  als makroskopische
Beziehung aufzufassen.
Aus Gl. (2.22) und (2.25) folgt:
als makroskopische
Beziehung aufzufassen.
Aus Gl. (2.22) und (2.25) folgt:

Die Leitungs- und Valenzbandkante  ,
,  haben keine quantenmechanische
Bedeutung.
Sie stellen Begrenzungen der Bewegung quasifreier Ladungsträger unter dem
Einfluß von Kräften dar [126].
haben keine quantenmechanische
Bedeutung.
Sie stellen Begrenzungen der Bewegung quasifreier Ladungsträger unter dem
Einfluß von Kräften dar [126].
Die physikalische Bedeutung der Bandkanten  ,
,  kann verdeutlicht
werden, wenn sie mit Hilfe der Vakuumniveaus
kann verdeutlicht
werden, wenn sie mit Hilfe der Vakuumniveaus  ,
,  , der
Elektronenaffinität
, der
Elektronenaffinität  und des Bandabstandes
und des Bandabstandes  dargestellt werden:
dargestellt werden:

In Gl. (2.28), (2.29) bezeichnet  die potentielle Energie
eines Elektrons
außerhalb des feldfreien Halbleiterkristalls (im Vakuum).
die potentielle Energie
eines Elektrons
außerhalb des feldfreien Halbleiterkristalls (im Vakuum).
 kann als lokales Vakuumniveau in Gegenwart
zusätzlicher Kraftfelder interpretiert werden.
Die Elektronenaffinität
kann als lokales Vakuumniveau in Gegenwart
zusätzlicher Kraftfelder interpretiert werden.
Die Elektronenaffinität  stellt die Energie dar, die aufgewendet werden
muß, um ein Elektron von der Leitungsbandkante zum lokalen Vakuumsniveau
zu befördern (
stellt die Energie dar, die aufgewendet werden
muß, um ein Elektron von der Leitungsbandkante zum lokalen Vakuumsniveau
zu befördern ( ).
).
 ist die Energiedifferenz zwischen dem Leitungsband und dem Valenzband.
ist die Energiedifferenz zwischen dem Leitungsband und dem Valenzband.
 kann als Bindungsenergie der äußersten
Valenzelektronen aufgefaßt werden.
kann als Bindungsenergie der äußersten
Valenzelektronen aufgefaßt werden.
Während das lokale Vakuumniveau Energieänderungen berücksichtigt, die
allen Bändern gemeinsam sind, können Elektronenaffinität und Bandabstand
zusätzliche lokale Änderungen der Energie des Leitungs- bzw.
Valenzbandes z.B. infolge einer ortsabhängigen Bandstruktur anzeigen
[126].




Next: 2.1.5 Die Zustandsdichte
Up: 2.1 Quantenmechanische Grundlagen
Previous: 2.1.3 Die effektive Masse
Martin Stiftinger
Sat Jun 10 15:00:12 MET DST 1995
 eingebaute
und angelegte Makropotentiale
eingebaute
und angelegte Makropotentiale  vorhanden.
Das eingebaute Potential ist durch inhomogene Dotierung bedingt, das angelegte
Potential ist auf die im jeweiligen Arbeitspunkt anliegende Spannung
zurückzuführen.
Das Verhalten eines einzelnen Kristallelektrons im Makropotential
vorhanden.
Das eingebaute Potential ist durch inhomogene Dotierung bedingt, das angelegte
Potential ist auf die im jeweiligen Arbeitspunkt anliegende Spannung
zurückzuführen.
Das Verhalten eines einzelnen Kristallelektrons im Makropotential  , das
dem Kristallpotential
, das
dem Kristallpotential  überlagert wird, ohne es zu beeinflussen,
kann von der Schrödingergleichung (2.1) beschrieben werden
(
überlagert wird, ohne es zu beeinflussen,
kann von der Schrödingergleichung (2.1) beschrieben werden
( ).
Nimmt man an, daß das von
).
Nimmt man an, daß das von  bedingte elektrische Feld zu schwach ist,
um Übergänge von einem Band in ein anderes zu induzieren,
läßt sich Gl. (2.1) (
bedingte elektrische Feld zu schwach ist,
um Übergänge von einem Band in ein anderes zu induzieren,
läßt sich Gl. (2.1) ( ) umformen [121]:
) umformen [121]:





 des periodischen Kristallpotentials explizit
nicht mehr.
Ersetzt man die Bandstruktur
des periodischen Kristallpotentials explizit
nicht mehr.
Ersetzt man die Bandstruktur  in Gl. (
in Gl. ( im Feld des Potentials
im Feld des Potentials
 gegebenen Dispersionsbeziehung zwischen
Energie und Wellenvektor.
Allerdings ist nicht zu vergessen, daß die Gültigkeit der
effektive-Masse-Näherung in Anwesenheit von Makropotentialen
streng genommen auf Elektronen in unmittelbarer
Nähe der Bandränder in schwachen, langsam veränderlichen Feldern
beschränkt bleibt
gegebenen Dispersionsbeziehung zwischen
Energie und Wellenvektor.
Allerdings ist nicht zu vergessen, daß die Gültigkeit der
effektive-Masse-Näherung in Anwesenheit von Makropotentialen
streng genommen auf Elektronen in unmittelbarer
Nähe der Bandränder in schwachen, langsam veränderlichen Feldern
beschränkt bleibt 
 stellt die Gesamtenergie
stellt die Gesamtenergie  eines
im gestörten Halbleiter als klassisches Teilchen betrachteten
Elektrons als Funktion des
Wellenvektors
eines
im gestörten Halbleiter als klassisches Teilchen betrachteten
Elektrons als Funktion des
Wellenvektors  (bzw. Impulses
(bzw. Impulses  )
und des Ortes
)
und des Ortes  dar.
Die Gesamtenergie setzt sich aus der Bandenergie
dar.
Die Gesamtenergie setzt sich aus der Bandenergie
 und der potentiellen Energie
und der potentiellen Energie  der externen
Störung zusammen.
Die Bandenergie
der externen
Störung zusammen.
Die Bandenergie  in Gl. (
in Gl. (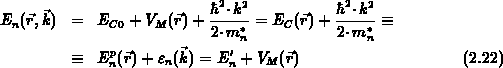
 ist die potentielle Energie des Elektrons im
ungestörten Kristall.
Der letzte Term ist die
ist die potentielle Energie des Elektrons im
ungestörten Kristall.
Der letzte Term ist die  ist die Leitungsbandkante.
Sie stellt die gesamte potentielle Energie dar.
ist die Leitungsbandkante.
Sie stellt die gesamte potentielle Energie dar.
 und der kinetischen Energie
und der kinetischen Energie  zusammen.
(Anmerkung: Obwohl in dieser Arbeit nur Standardbänder betrachtet
werden, wird
zusammen.
(Anmerkung: Obwohl in dieser Arbeit nur Standardbänder betrachtet
werden, wird  geschrieben).
geschrieben).



 stellt die energetischen Verhältnisse für den
Grenzfall des ruhenden Elektrons (oder Lochs) (
stellt die energetischen Verhältnisse für den
Grenzfall des ruhenden Elektrons (oder Lochs) ( ) dar.
Während die Bandstruktur
) dar.
Während die Bandstruktur  als makroskopische
Beziehung aufzufassen.
Aus Gl. (
als makroskopische
Beziehung aufzufassen.
Aus Gl. (
 haben keine quantenmechanische
Bedeutung.
Sie stellen Begrenzungen der Bewegung quasifreier Ladungsträger unter dem
Einfluß von Kräften dar
haben keine quantenmechanische
Bedeutung.
Sie stellen Begrenzungen der Bewegung quasifreier Ladungsträger unter dem
Einfluß von Kräften dar  ,
,  , der
Elektronenaffinität
, der
Elektronenaffinität  und des Bandabstandes
und des Bandabstandes  dargestellt werden:
dargestellt werden:

 kann als lokales Vakuumniveau in Gegenwart
zusätzlicher Kraftfelder interpretiert werden.
Die Elektronenaffinität
kann als lokales Vakuumniveau in Gegenwart
zusätzlicher Kraftfelder interpretiert werden.
Die Elektronenaffinität  ).
).
 kann als Bindungsenergie der äußersten
Valenzelektronen aufgefaßt werden.
kann als Bindungsenergie der äußersten
Valenzelektronen aufgefaßt werden.