Footnotes
- ...
 differs completely from the intrinsic level in the gate
associated with
differs completely from the intrinsic level in the gate
associated with  and
and  , but is connected with
, but is connected with
 and
and  (Figure 2.3). We are in
accord with the critical discussion in [291].
(Figure 2.3). We are in
accord with the critical discussion in [291].
- ...
- The quasi-neutral approximation is valid in a
non-compensated semiconductor if the dopant concentration does not vary to much
over the local Debye length comparing with its absolute value. In particular,
considering gaussian and exponential distributions for an assumed concentration
at the gate-contact of
 and minimal polysilicon thickness of
and minimal polysilicon thickness of
 , we find that the quasi-neutral approximation is fulfilled in the gate
for doping levels at the gate/oxide interface higher than about
, we find that the quasi-neutral approximation is fulfilled in the gate
for doping levels at the gate/oxide interface higher than about
 , but it is not satisfied at lower doping levels.
, but it is not satisfied at lower doping levels.
- ...
- Experimental data is kindly provided by B.Fishbein from
Digital Equipment Corp. at Hudson (MA).
- ...
- Statistical variations in
 may influence
our analysis. We suppose this effect is negligible here.
may influence
our analysis. We suppose this effect is negligible here.
- ...
- Due to a zero current-component
perpendicular to the interface, the mobility vanishes from the continuity
equations and the problem reduces to the one-dimensional Poisson equation only.
The perturbation induced by a small current along the channel is negligible with
respect to
 ,
,  ,
,  and
and  .
.
- ...
- Fig.7 in [367] is recalculated with
respect to
 ; the bias at which the gate becomes inverted is
calculated for given device data.
; the bias at which the gate becomes inverted is
calculated for given device data.
- ...
- This effect is well
exploited in several measurement techniques applicable on small MOSFETs, as the
split
 -
- [442][256], the small-signal
input-conductance [178] and transadmittance [177] methods,
and the split-current method [115] which are reviewed in
Section 3.1.2.
[442][256], the small-signal
input-conductance [178] and transadmittance [177] methods,
and the split-current method [115] which are reviewed in
Section 3.1.2.
- ...
- Heavy-doping effects have been neglected in this
analytical calculation.
- ...
- From the theoretical point of view, when the
carriers drift with the saturation velocity the charge is uniformly, the
potential parabolically and the field linearly distributed in this region,
independent of the gate bias [266][161].
- ...
- Note that the
variation of
 with
with  , or more precisely with effective transversal
field
, or more precisely with effective transversal
field  , has a weaker effect in thin-oxide devices than in
thick-oxide devices, since in the former devices the transversal fields are
stronger than in the latter. As is well known, due to a quantum-mechanical
broadening of the inversion layer the slope of
, has a weaker effect in thin-oxide devices than in
thick-oxide devices, since in the former devices the transversal fields are
stronger than in the latter. As is well known, due to a quantum-mechanical
broadening of the inversion layer the slope of  reduces
at high fields ([413]).
reduces
at high fields ([413]).
- ...
- at room temperatures. At low temperatures
 can be
an increasing function at low fields.
can be
an increasing function at low fields.
- ...
- This calculation corresponds to that given in
Figure 2.6 for
 -gate/
-gate/ -type of bulk. Note that in
MOSFET,
-type of bulk. Note that in
MOSFET,  is also influenced by the vicinity of the source junction.
is also influenced by the vicinity of the source junction.
- ...
- This difference arises due to
 in real devices, which is a consequence of a weak
saturation in the
in real devices, which is a consequence of a weak
saturation in the  characteristic for holes, a particularly emphasized
effect when
characteristic for holes, a particularly emphasized
effect when  is low due to high normal
field [443][162].
is low due to high normal
field [443][162].
- ...
- The author
of [332] claims he and his colleague were the first to discover the
charge-pumping effect, referring to the patent [148]. The
work [43] was submitted for publication on July 11, 1968; revised on
December 4, 1968 and published in March 1969. The patent [148] was
filed on October 17, 1968 and issued on August 4, 1970.
- ...
- Note that, although we have written
 and
and  in
Figures 3.2, 3.3, we are here speaking
about the charge-pumping threshold voltage and the charge-pumping
flat-band potential. Different definitions and denotations for these
voltages shall be introduced later in Section 3.3.
in
Figures 3.2, 3.3, we are here speaking
about the charge-pumping threshold voltage and the charge-pumping
flat-band potential. Different definitions and denotations for these
voltages shall be introduced later in Section 3.3.
- ...
- In charge-pumping theory we assume for the midgap, the energy level
where the generation rates of electrons and holes are equal to
each other:
 .
.
- ...
- Of course, by using the waveform as in
Figure 3.3 but reversed in time the lower part
of the band gap can be scanned.
- ...
- An experimental setup for the RTS measurements is given
in [219].
- ...
- Evidently, the density distribution in the
position and the energy space
 has lost its meaning
here.
has lost its meaning
here.
- ...
- The nomenclature for currents and voltages is
explained at the end of the symbol list.
- ...
- In the conventional
charge-pumping method the same extrapolation technique yields
 only.
only.
- ...
- This idea is known from the comparative QS-HF
 -
- technique.
technique.
- ...
- Although this local shift can exhibit several
volts, it can produce only slight changes in device characteristics.
- ...
- Some examples are given while discussing the
hot-carrier degradation in Section 3.5.
- ...
- The electron capture cross-sections for the 2D quantum model
 found in [432] are one order of
magnitude larger than those for the classical 3D model! This difference
seems to be, however, not so important in practice, because we always use
the capture cross-sections determined consistently with the theory
assumed. For instance, although the quantum effects are rather pronounced
in the MOS inversion layer at room temperature, giving quite different
carrier-distributions than the classical theory, the differences in the
total inversion-layer charge are small. In fact, we can either apply
e.g. the classical carrier distribution with the corresponding
surface mobility or the quantum-mechanical carrier distribution with
the quantum-mechanical surface mobility. Since the parameters for both
mobility models are determined by fitting the channel conductivity
anyway, we can use the classical model to calculate the current-voltage
characteristics.
found in [432] are one order of
magnitude larger than those for the classical 3D model! This difference
seems to be, however, not so important in practice, because we always use
the capture cross-sections determined consistently with the theory
assumed. For instance, although the quantum effects are rather pronounced
in the MOS inversion layer at room temperature, giving quite different
carrier-distributions than the classical theory, the differences in the
total inversion-layer charge are small. In fact, we can either apply
e.g. the classical carrier distribution with the corresponding
surface mobility or the quantum-mechanical carrier distribution with
the quantum-mechanical surface mobility. Since the parameters for both
mobility models are determined by fitting the channel conductivity
anyway, we can use the classical model to calculate the current-voltage
characteristics.
- ...
- Note,
this model is for MOSFETs and not for MOS capacitors.
- ...
- The factor
 in 3.7
equals to
in 3.7
equals to  for shallow acceptor-like bulk traps and to
for shallow acceptor-like bulk traps and to  for
shallow donor-like bulk traps, where
for
shallow donor-like bulk traps, where  and
and  denote the trap
degeneracy. In Si,
denote the trap
degeneracy. In Si,  and
and  . It is not trivial to determine
. It is not trivial to determine  for
interface traps in MOS structures (cf. [149]).
for
interface traps in MOS structures (cf. [149]).
- ...
- For each
trap level
 , only the transitions
, only the transitions  and
and  are allowed.
are allowed.
- ...
- This statement has been proven in [314] assuming
vanishing generation-recombination.
- ...
- The residual error in the Poisson equation
 becomes for
e.g. 3.17 - 3.19:
becomes for
e.g. 3.17 - 3.19:
 , where
, where  is the
residual error at
is the
residual error at  . In spite of
. In spite of  at the beginning of transient
simulation,
at the beginning of transient
simulation,  accumulates with progressing in time, at each step with
accumulates with progressing in time, at each step with
 . Note that the trap-related quantities vanish from
. Note that the trap-related quantities vanish from  because
of
because
of  .
.
- ...
- In special cases, the error
function and the Dawson integral can be obtained.
- ...
- An equidistant discretization in
the energy space seems to be the best a priori choice, because all trap
levels play similar role in determining the device characteristics, contrary
to the enormous differences in their time constants. Indeed, we vary the
characteristic time intervals in the gate waveform in an exponential range to
characterize the particular intervals on the energy scale.
- ...
- For e.g. the bulk electron current
the averaging consistent with 3.18 reads
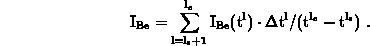
- ...
- This definition is improper
for the waveform with
 or
or  . In these cases, a
slight capture during the pulse edges can dominate over the capture during the
top level, in spite of an exponentially varying
. In these cases, a
slight capture during the pulse edges can dominate over the capture during the
top level, in spite of an exponentially varying  . An example is
given in Figure 3.7.
. An example is
given in Figure 3.7.
- ...
- For
example, the case
 and
and  is not
accounted for when considering the electron emission.
is not
accounted for when considering the electron emission.
- ...
- For
 -channel devices,
-channel devices,  must be in inversion and
must be in inversion and  is varied.
is varied.
- ...
- Both papers employ
a linear extrapolation of the curve
 , where
, where  is the gate
length, to examine the spatial uniformity of the traps in MOSFETs.
Particularly, [480] claims that zero intercept with both axes of
the linearly extrapolated curve may serve as proof that the traps
are uniformly distributed from the channel to the region deep in the
junctions.
Our rigorous analysis, not presented here, shows
that the latter claim is only correct if the hole-capture boundaries exactly
match the gate edges (
is the gate
length, to examine the spatial uniformity of the traps in MOSFETs.
Particularly, [480] claims that zero intercept with both axes of
the linearly extrapolated curve may serve as proof that the traps
are uniformly distributed from the channel to the region deep in the
junctions.
Our rigorous analysis, not presented here, shows
that the latter claim is only correct if the hole-capture boundaries exactly
match the gate edges ( -channel devices). It is, however, difficult to
fulfill this condition in practice. We think that monitoring the
-channel devices). It is, however, difficult to
fulfill this condition in practice. We think that monitoring the
 characteristics may provide reliable information on the uniformity
in the channel region, but not in the junctions, which is particularly
interesting.
characteristics may provide reliable information on the uniformity
in the channel region, but not in the junctions, which is particularly
interesting.
- ...
- We agree with
the comment in section 4.4.3 [504] that increasing interface trap
density with increasing bulk doping, detected in experiments in [441],
could be partially due to carriers localized in the deep band tails (see
discussion in Section 2.3.2).
- ...
- All experimental data presented
in this section is kindly provided by G.Groeseneken and his colleagues at
IMEC, Leuven (Belgium).
- ...
- When the junctions are biased with
respect to the bulk and the gate pulse fails on the bottom level we have
the conditions typical for the GIDL effect (Section 4.1).
- ...
- The oxide thickness can increase locally due to
the gate reoxidation.
- ...
- Because the width of the depletion region is small in
the junctions, the local approximation
 becomes very accurate, regarding the effect elaborated in
Appendix F.
becomes very accurate, regarding the effect elaborated in
Appendix F.
- ...
 is variable in the simulation. It is limited
at the rising and falling edges of the gate pulse:
is variable in the simulation. It is limited
at the rising and falling edges of the gate pulse:
 . At the top and bottom level,
. At the top and bottom level,  increases
progressively.
increases
progressively.
- ...
 changes exponentially with the surface potential in
depletion and weak inversion.
changes exponentially with the surface potential in
depletion and weak inversion.
- ...
- on Hewlett Packard 9000/720, one signal period in 79 steps.
- ...
- The
pinch-off here refers to the
 -coordinate where the oxide field
changes in direction.
-coordinate where the oxide field
changes in direction.
- ...
- The source-sided gate edge is the origin.
- ...
- The transition between the steady-state and the
non-steady-state emission does not coincide with the transition between strong
and weak inversion at the interface. These two effects are completely
different, as is explained through in Section 3.3. However,
for common physical parameters and switching in the
 -range the former
effect typically occurs as a consequence of the latter.
-range the former
effect typically occurs as a consequence of the latter.
- ...
- This effect cannot be clearly
seen in Figure D.1; it can be well observed when the gate
bottom level is sufficiently high.
- ...
- Rigorously
speaking, these areas are not equal. In this case, the difference is
 and
and  at the rising and falling edge,
respectively.
at the rising and falling edge,
respectively.
- ...
- The lateral current flow can influence the
gate/drain fringing problem to a considerable degree at high current
levels [356][355].
- ...
- when both curves are reduced on the same
gate-pulse level, with other words when the electron curve is shifted
downwards by the pulse amplitude
- ...
- Doping is nonuniform close to the drain
contact in the analyzed LDD device. The reference level for
 in the
numerical results is chosen deeply in the drain area. For calculations in
Figure E.5 this area is assumed to be uniformly doped in the
concentration equaling to the surface concentration in the LDD region.
in the
numerical results is chosen deeply in the drain area. For calculations in
Figure E.5 this area is assumed to be uniformly doped in the
concentration equaling to the surface concentration in the LDD region.
- ...
- The problem can be reduced to the
properties of
 and
and  functions [152].
functions [152].
- ...
- To perform this calculation an iterative loop with respect
to
 is implemented in MINIMOS, like the loop used for the
threshold voltage calculation.
is implemented in MINIMOS, like the loop used for the
threshold voltage calculation.
- ...
- We
have assumed bulk depletion. In general, the superposition theorem cannot be
applied because
 is not a linear function.
is not a linear function.
- ...
- In LDD devices, due to the
LDD field-peak at the source side, some damage can occur near the source
junction as well!
- ...
- this assumption is standard. We have shown in Appendix F
that the real situation is much more complicated for the strongly localized
charge. Differences in shift of e.g.
 and
and  can be
expected due to different depletion layer width in these cases.
can be
expected due to different depletion layer width in these cases.
- ...
- This value depends on the
magnitude of the corresponding interband matrix element for the
phonon-scattering in Si. We assumed
 .
.
- ...
- The valence
band edge is the origin of the energy axis
Martin Stiftinger
Sat Oct 15 22:05:10 MET 1994
 differs completely from the intrinsic level in the gate
associated with
differs completely from the intrinsic level in the gate
associated with  and
and  , but is connected with
, but is connected with
 and
and  (Figure 2.3). We are in
accord with the critical discussion in [291].
(Figure 2.3). We are in
accord with the critical discussion in [291]. and minimal polysilicon thickness of
and minimal polysilicon thickness of
 , we find that the quasi-neutral approximation is fulfilled in the gate
for doping levels at the gate/oxide interface higher than about
, we find that the quasi-neutral approximation is fulfilled in the gate
for doping levels at the gate/oxide interface higher than about
 , but it is not satisfied at lower doping levels.
, but it is not satisfied at lower doping levels. may influence
our analysis. We suppose this effect is negligible here.
may influence
our analysis. We suppose this effect is negligible here. ,
,  ,
,  and
and  .
. ; the bias at which the gate becomes inverted is
calculated for given device data.
; the bias at which the gate becomes inverted is
calculated for given device data. -
- [442][256], the small-signal
input-conductance [178] and transadmittance [177] methods,
and the split-current method [115] which are reviewed in
Section 3.1.2.
[442][256], the small-signal
input-conductance [178] and transadmittance [177] methods,
and the split-current method [115] which are reviewed in
Section 3.1.2. with
with  , or more precisely with effective transversal
field
, or more precisely with effective transversal
field  , has a weaker effect in thin-oxide devices than in
thick-oxide devices, since in the former devices the transversal fields are
stronger than in the latter. As is well known, due to a quantum-mechanical
broadening of the inversion layer the slope of
, has a weaker effect in thin-oxide devices than in
thick-oxide devices, since in the former devices the transversal fields are
stronger than in the latter. As is well known, due to a quantum-mechanical
broadening of the inversion layer the slope of  reduces
at high fields ([413]).
reduces
at high fields ([413]). can be
an increasing function at low fields.
can be
an increasing function at low fields. -gate/
-gate/ -type of bulk. Note that in
MOSFET,
-type of bulk. Note that in
MOSFET,  is also influenced by the vicinity of the source junction.
is also influenced by the vicinity of the source junction. in real devices, which is a consequence of a weak
saturation in the
in real devices, which is a consequence of a weak
saturation in the  characteristic for holes, a particularly emphasized
effect when
characteristic for holes, a particularly emphasized
effect when  is low due to high normal
field [443][162].
is low due to high normal
field [443][162]. and
and  in
Figures 3.2, 3.3, we are here speaking
about the charge-pumping threshold voltage and the charge-pumping
flat-band potential. Different definitions and denotations for these
voltages shall be introduced later in Section 3.3.
in
Figures 3.2, 3.3, we are here speaking
about the charge-pumping threshold voltage and the charge-pumping
flat-band potential. Different definitions and denotations for these
voltages shall be introduced later in Section 3.3. .
. has lost its meaning
here.
has lost its meaning
here. only.
only. -
- technique.
technique. found in [432] are one order of
magnitude larger than those for the classical 3D model! This difference
seems to be, however, not so important in practice, because we always use
the capture cross-sections determined consistently with the theory
assumed. For instance, although the quantum effects are rather pronounced
in the MOS inversion layer at room temperature, giving quite different
carrier-distributions than the classical theory, the differences in the
total inversion-layer charge are small. In fact, we can either apply
e.g. the classical carrier distribution with the corresponding
surface mobility or the quantum-mechanical carrier distribution with
the quantum-mechanical surface mobility. Since the parameters for both
mobility models are determined by fitting the channel conductivity
anyway, we can use the classical model to calculate the current-voltage
characteristics.
found in [432] are one order of
magnitude larger than those for the classical 3D model! This difference
seems to be, however, not so important in practice, because we always use
the capture cross-sections determined consistently with the theory
assumed. For instance, although the quantum effects are rather pronounced
in the MOS inversion layer at room temperature, giving quite different
carrier-distributions than the classical theory, the differences in the
total inversion-layer charge are small. In fact, we can either apply
e.g. the classical carrier distribution with the corresponding
surface mobility or the quantum-mechanical carrier distribution with
the quantum-mechanical surface mobility. Since the parameters for both
mobility models are determined by fitting the channel conductivity
anyway, we can use the classical model to calculate the current-voltage
characteristics. in 3.7
equals to
in 3.7
equals to  for shallow acceptor-like bulk traps and to
for shallow acceptor-like bulk traps and to  for
shallow donor-like bulk traps, where
for
shallow donor-like bulk traps, where  and
and  denote the trap
degeneracy. In Si,
denote the trap
degeneracy. In Si,  and
and  . It is not trivial to determine
. It is not trivial to determine  for
interface traps in MOS structures (cf. [149]).
for
interface traps in MOS structures (cf. [149]). , only the transitions
, only the transitions  and
and  are allowed.
are allowed. becomes for
e.g. 3.17 - 3.19:
becomes for
e.g. 3.17 - 3.19:
 , where
, where  is the
residual error at
is the
residual error at  . In spite of
. In spite of  at the beginning of transient
simulation,
at the beginning of transient
simulation,  accumulates with progressing in time, at each step with
accumulates with progressing in time, at each step with
 . Note that the trap-related quantities vanish from
. Note that the trap-related quantities vanish from  because
of
because
of  .
.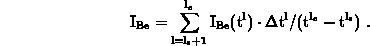
 or
or  . In these cases, a
slight capture during the pulse edges can dominate over the capture during the
top level, in spite of an exponentially varying
. In these cases, a
slight capture during the pulse edges can dominate over the capture during the
top level, in spite of an exponentially varying  . An example is
given in Figure 3.7.
. An example is
given in Figure 3.7. and
and  is not
accounted for when considering the electron emission.
is not
accounted for when considering the electron emission. -channel devices,
-channel devices,  must be in inversion and
must be in inversion and  is varied.
is varied. , where
, where  is the gate
length, to examine the spatial uniformity of the traps in MOSFETs.
Particularly, [480] claims that zero intercept with both axes of
the linearly extrapolated curve may serve as proof that the traps
are uniformly distributed from the channel to the region deep in the
junctions.
Our rigorous analysis, not presented here, shows
that the latter claim is only correct if the hole-capture boundaries exactly
match the gate edges (
is the gate
length, to examine the spatial uniformity of the traps in MOSFETs.
Particularly, [480] claims that zero intercept with both axes of
the linearly extrapolated curve may serve as proof that the traps
are uniformly distributed from the channel to the region deep in the
junctions.
Our rigorous analysis, not presented here, shows
that the latter claim is only correct if the hole-capture boundaries exactly
match the gate edges ( -channel devices). It is, however, difficult to
fulfill this condition in practice. We think that monitoring the
-channel devices). It is, however, difficult to
fulfill this condition in practice. We think that monitoring the
 characteristics may provide reliable information on the uniformity
in the channel region, but not in the junctions, which is particularly
interesting.
characteristics may provide reliable information on the uniformity
in the channel region, but not in the junctions, which is particularly
interesting. becomes very accurate, regarding the effect elaborated in
Appendix F.
becomes very accurate, regarding the effect elaborated in
Appendix F. is variable in the simulation. It is limited
at the rising and falling edges of the gate pulse:
is variable in the simulation. It is limited
at the rising and falling edges of the gate pulse:
 . At the top and bottom level,
. At the top and bottom level,  increases
progressively.
increases
progressively. changes exponentially with the surface potential in
depletion and weak inversion.
changes exponentially with the surface potential in
depletion and weak inversion. -coordinate where the oxide field
changes in direction.
-coordinate where the oxide field
changes in direction. -range the former
effect typically occurs as a consequence of the latter.
-range the former
effect typically occurs as a consequence of the latter. and
and  at the rising and falling edge,
respectively.
at the rising and falling edge,
respectively. in the
numerical results is chosen deeply in the drain area. For calculations in
Figure E.5 this area is assumed to be uniformly doped in the
concentration equaling to the surface concentration in the LDD region.
in the
numerical results is chosen deeply in the drain area. For calculations in
Figure E.5 this area is assumed to be uniformly doped in the
concentration equaling to the surface concentration in the LDD region. and
and  functions [152].
functions [152]. is implemented in MINIMOS, like the loop used for the
threshold voltage calculation.
is implemented in MINIMOS, like the loop used for the
threshold voltage calculation. is not a linear function.
is not a linear function. and
and  can be
expected due to different depletion layer width in these cases.
can be
expected due to different depletion layer width in these cases. .
.