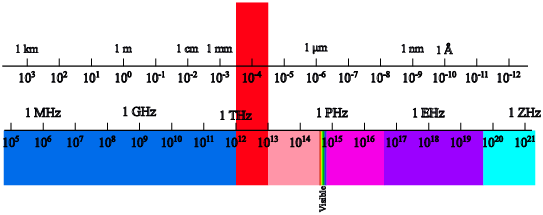
| Figure 2.1: The terahertz spectrum is located between the optical domain and the microwave domain. |



For more than 35 years, semiconductor nanostructures have been investigated for a large number of applications in technology including lasers, photodetectors, light emitting diodes, and transistors. Nowadays, these structures are considered to be even more perspective for novel applications. This is why after such a long period the intensive research performed in this field even grows further.
If the geometrical extent of a semiconductor, typically embedded in the matrix of another semiconductor, is reduced in one, two or three directions of space below the size of the "de Broglie wavelength" of a charge carrier which is on the order of a few nanometers, it is called a nanostructure [1].
The electrical and optical properties of low-dimensional structures, including their interactions such as electron-electron, electron-hole, and electron-photon interaction, depend qualitatively on the dimensionality of the structure and quantitatively on details of the geometry of the structure such as size and shape, and on the distribution of the atoms inside [1]. The electronic properties in turn control the linear and nonlinear optical and electronic transport properties. Thus "geometrical architecture" opens enormous opportunities for designing completely novel materials or heterostructures.
The far-infrared (FIR) frequency range is roughly defined as 30-300 µ m or 4-40 meV and is often referred to as the terahertz frequency range 1-10 THz [2, 3, 4], see Fig. 2.1. FIR electromagnetic radiation is important in many applications such as radio astronomy, environmental monitoring, plasmon diagnostics, laboratory spectroscopy, telecommunications, medicine etc. and in the characterization of nanoscale condensed matter materials. In recent years, the generation, propagation and detection of FIR electromagnetic radiation using two-dimensional semiconductor systems or other semiconductor nanostructures has become one of the most rapidly expanding fields in photonics, optoelectronics and condensed matter physics.

Figure 2.1: The terahertz spectrum is located between the optical domain and the microwave domain.
However, the terahertz frequency range cannot be directly accessed. Diode lasers are ideal sources because they are cheap, compact and very efficient. However, the semiconductor bandgap places a limitation on emission frequency. The longest-wavelength diode lasers (∼ 30µ m) are based on narrow gap lead-salt semiconductors [5]. While these lead-salt lasers have been quite successful for high resolution spectroscopy, they are still limited to cryogenic operation and provide relatively low power. On the other end of the spectrum, semiconductor transistors can be used to generate 100 GHz oscillators [6]. Molecular gas lasers are one of the practical laser sources for the FIR, but they have limited lasing frequencies. They are also somewhat unwieldy as they require high voltage supplies and are usually rather bulky.
Semiconductor nanostructures are most promising candidates to solve the lack of suitable sources and detectors in the FIR frequency range. Graphene nanostructures [7, 8, 9, 10, 11, 12] and quantum cascade devices [13, 14, 15, 16, 17, 18, 19, 20, 21, 22] promise efficient operation in a broad frequency range. Electronically, pure graphene is a gapless semiconductor. Since the potential usefulness of graphene in electronic and photonic applications cannot be fully tapped unless a bandgap can be engineered, bandgap engineering of graphene has attracted much research interest recently. In gapped graphene, a vertical linear response peak is predicted when the photon frequency matches the bandgap energy. Stripped into a few nanometer-wide graphene nanoribbon, the bandgap can be tuned to a certain extent by the confinement of electronic wave function. One dimensional graphene nanoribbons and superlattices provide precise tunable energy gaps for optical applications.
Bandgap engineering of graphene-based structures could result in devices operating in the terahertz domain. Bandgap engineering for terahertz operation is also possible in intersubband quantum cascade heterostructures [23]. Intersubband optical devices have several advantages over conventional interband semiconductor devices. Most useful is the fact that the emission frequency is determined by the design of the heterostructure and can hence be tailored to the application. This is especially useful for infrared applications where small bandgap materials become difficult to find and work with. Also, since the envelope functions extend over a well (tens of Angstroms), the dipole moment for the intersubband transition is typically several orders of magnitude larger than that of an atomic transition.
In October 2004, graphene, a one-atomic layer of carbon with a honeycomb structure, started a revolution in science and technology. Physicists reported that they had prepared graphene and observed the electric field effect in their samples [24]. Shortly after, this new material attracted the attention in many areas of research including condensed matter, material physics, chemistry, and device physics. Graphene-based structures such as graphene nanoribbons (GNRs) [25], nanorods [26] quantum dots [27], and p-n junctions [28] have been successfully fabricated.
To understand graphene in more details, it is useful to consider it as the single layer limit of graphite (Fig.2.2). In this light, the extraordinary properties of honeycomb carbon are not really new. Abundant and naturally occurring, graphite has been known as a mineral for nearly 500 years. Even in the middle ages, the layered morphology and weak dispersion forces between adjacent sheets were utilized to make marking instruments, much in the same way that we use graphite in pencils today. More recently, these same properties have made graphite an ideal material for use as a dry lubricant, along with the similarly structured but more expensive compounds hexagonal boron nitride and molybdenum disulfide [29].
An extraordinarily high carrier mobility of more than 2×105 cm2/Vs [30, 31, 32] makes graphene a major candidate for future electronic applications. Today a growing number of groups are successfully fabricating graphene transistors [33]. Major chip-makers are now active in graphene research and the International Technology Roadmap for Semiconductors, the strategic planning document for the semiconductor industry, considers graphene to be among the candidate materials for post-silicon electronics [34] and terahertz applications [35]. Graphene is also regarded as a pivotal material in the emerging field of spin electronics due to spin coherence even at room temperature [36, 37].
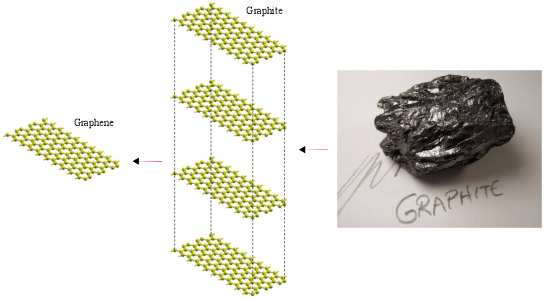
Figure 2.2: Graphene is a single layer honeycomb lattice of carbon atoms. Graphite can be viewed as a stack of graphene layers.
One of the many interesting properties of Dirac electrons in graphene is the drastic change of the conductivity of graphene-based structures with the confinement of electrons. Structures that realize this behavior are carbon nanotubes (CNTs) and graphene nanoribbons (GNRs), which impose periodic and zero boundary conditions, respectively, on the transverse electron wave-vector. In CNT-based devices control over the chirality and diameter and thus of the associated electronic bandgap remains a major technological problem. GNRs do not suffer from this problem and are thus recognized as promising building blocks for nanoelectronic devices [38]. GNRs less than 10nm wide with ultrasmooth edges have been fabricated [39].
GNRs can be considered as a graphene sheet tailored along a certain direction and can be accordingly classified as of armchair or zigzag shape, see Fig. 2.3(a) and (b). Tight-binding calculations predict that ZGNRs are always metallic while AGNRs may be either metallic or semiconducting depending on their direction and width [40, 41]. The edges of GNRs can significantly affect the electronic properties of the ribbon. In the electronic band structure of GNRs with zigzag edges a flat band, which corresponds to localized states at the edges, appears around the Fermi level [41, 42]. However, such states do not appear in GNRs with armchair edges (AGNRs) [41].
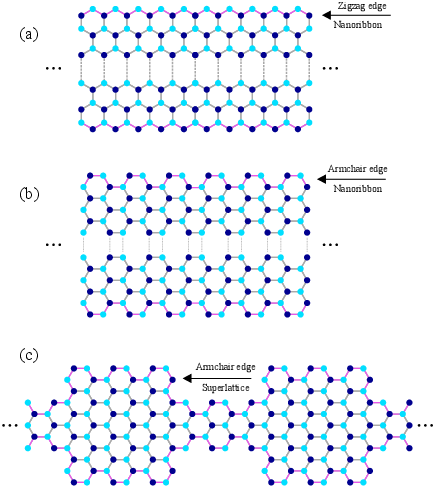
Figure 2.3: Schematic of (a) zigzag and (b) armchair edge configurations of GNRs. The position of the edge is indicated by the pink line. (c) An armchair edge graphene superlattice structure.
The controllable alteration of graphene by high-precision lithography [43, 44, 39] and chemical functionalization [45] has enabled modulation of the electronics, optical and thermal properties of these structures. A recent experimental study has reported ultra-smooth patterning of graphene nanoribbons with modulated widths which can be regarded as finite segments of GNR-based superlattices [39], see Fig. 2.3(c). Such structures can behave as multiple quantum wells and exhibit interesting quantum effects [46] such as resonant tunneling [47].
Due to possible application in nanoelectronics [38], photonics [48, 49], and spintronics [50], intensive scientific research is being carried out on graphene-based structures.
Graphene is composed of carbon atoms arranged in a hexagonal structure, as shown in Fig. 2.4. The structure can be seen as a triangular lattice with a basis of two atoms per unit cell. The lattice vectors can be written as
| a1= |
| (3, | √ |
| ), a2= |
| (3,− | √ |
| ) (1) |
where a≈1.42 Å is the carbon-carbon bond length. The reciprocal lattice vectors are given by
| b1= |
| (1, | √ |
| ), b2= |
| (1,− | √ |
| ) (2) |
Of particular importance for the physics of graphene are the two points K and K′ at the corners of the Brillouin zone. These are named Dirac points for reasons that will become clear later. Their positions in momentum space are given by
| K= | ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ |
| , |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ | , K′= | ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ |
| ,− |
| ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ | (3) |
The three nearest-neighbor vectors in real space are
| δ1 = |
| (1, | √ |
| ), δ2 = |
| (1,− | √ |
| ), δ3 = −a(1,0) (4) |
while the six second-nearest neighbors are located at δ′1=± a1, δ′2=± a2, δ′3=± (a2−a1). The tight-binding Hamiltonian for electrons in graphene considering that electrons can hop to both nearest- and next-nearest-neighbor atoms has the form (we use units such that ℏ=1)
| H = −t |
| ⎛ ⎝ | aσ,i†bσ,i+H.c. | ⎞ ⎠ | −t′ |
| ⎛ ⎝ | aσ,i†aσ,i+bσ,i†bσ,i+H.c. | ⎞ ⎠ | , (5) |
where aσ,i annihilates an electron with spin σ (σ=↑,↓) and aσ,i† creates an electron with spin σ on site Ri on sublattice A. An equivalent definition is used for sublattice B. The nearest-neighbor hopping energy between different sublattices is t≈2.7 eV, and t′ is the next nearest-neighbor hopping energy in the same sublattice. The value of t′ is not well known but ab initio calculations [51] indicate 0.02t≲ t′≲ 0.2t depending on the tight-binding parametrization. These calculations also include the effect of third-nearest-neighbors hopping, which has a hopping parameter of around 0.07 eV. A tight-binding fit to cyclotron resonance experiments [52] gives t′≈0.1 eV.
The two-dimensional energy dispersion relations of graphene can be calculated by solving the eigen-value problem for the Hamiltonian. In the Slater-Koster scheme [53] one gets
| H = | ⎡ ⎢ ⎣ |
| ⎤ ⎥ ⎦ | , (6) |
where
| f(k)=−t | ⎛ ⎝ | 1+eik·a1+eik·a2 | ⎞ ⎠ | =−t | ⎛ ⎜ ⎜ ⎝ | 1+2e |
| cos | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ | ⎞ ⎟ ⎟ ⎠ | . (7) |
Solution of the secular equation det(H−EI)=0 leads to the spectrum
| E±(k)=± t |
|
| , (8) |
which is symmetric around zero energy. Here, t′=0 was assumed.
Electrical conduction is determined by the states around the Fermi energy and so it is useful to develop an approximate relation that describes the linear dispersion relation around E=0. This can be done by replacing the expression for Eq. 7 with a Taylor expansion around one Dirac point k=K where the energy gap is zero. To simplify the derivation, we define a new wave vector relative to K which is called k′
| k′ = k − K = (kx− |
| ,ky− |
| ), (9) |
so we have
| f(k′)=−t | ⎛ ⎜ ⎜ ⎝ | 1−2e |
| cos | ⎛ ⎜ ⎜ ⎝ |
| + |
| ⎞ ⎟ ⎟ ⎠ | ⎞ ⎟ ⎟ ⎠ | . (10) |
Now we consider the dispersion relation E(k′) which hols E(0)=0. The Taylor expansion for new wave vector around (0,0) gives
| f ≈ k′x | ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ |
| + k′y | ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ |
| . (11) |
It is straightforward to evaluate the partial derivatives
| ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ |
| = |
| , | ⎡ ⎢ ⎢ ⎣ |
| ⎤ ⎥ ⎥ ⎦ |
| =− |
| , (12) |
therefore
| f(k′) ≈ |
| (k′x + ik′y). (13) |
The corresponding energy dispersion relation (Eq. 8) shows a linear dependence on the relation wavenumber | k′| =√k′x2+k′y2
| E(k′)=± | f(k′)| =± |
| | k′| (14) |
Figure 2.5 shows the electronic energy dispersion relations for graphene as a function of the two-dimensional wave-vector k in the hexagonal Brillouin zone. For finite values of t′, the electron-hole symmetry is broken and the π and π* bands become asymmetric.
The points K and K′, which specify six locations in momentum space, are called Dirac points, see Fig. 2.5. The conduction and valence bands meet at the Dirac points so graphene is a zero-gap material. The term "massless Dirac fermions" is used to refer to linear dispersion relation E±(k) in Eq. 14. Electrons propagating through graphene behave as massless Dirac fermions because of the linear relation between their energy and their momentum [54].
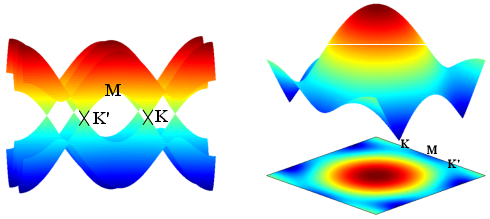
Figure 2.5: The energy dispersion relations for graphene are shown through the whole region of the Brillouin zone. The lower and the upper surfaces denote the valence π and the conduction π * energy bands, respectively. The coordinates of high symmetry points are Γ =(0,0), K=(2π/3a,2π/3√3a), and M=(2π/3a,0). The energy values at the K, M, and Γ points are 0, t, and 3t, respectively.
Graphene has interesting properties which allow multiple functions of signal emitting, transmitting, modulating, and detection to be realized in one material. Graphene shows superior properties compared to silicon and III-V semiconductors in terms of its high thermal conductivity (∼ 36 times higher than Si and ∼ 100 times higher than GaAs), high optical damage threshold [55] (a few orders of magnitude higher than Si [56] and GaAs [57]), and high third-order optical nonlinearities (∼ 3.3×10−16 coulomb) [58, 59].
Due to the unique electronic structure in which conical-shaped conduction and valence bands meet at the Dirac point (Fig. 2.5), the optical conductance of pristine monolayer graphene is frequency-independent in a broad range of photon energies [60]. It is argued [61, 62] that the high-frequency (dynamic) conductivity G for Dirac fermions [63] in graphene should be a universal constant equal to [64]
| Gl(ω)=G0≡ e2/4ℏ, (15) |
where index "l" refers to the real part, ω is the radian frequency, e is electron charge, and ℏ is reduced Planck’s constant. As a direct consequence of this universal optical conductance, the optical transmittance of pristine graphene is also frequency-independent and solely determined by the fine structure constant α=(1/4πє0)(e2/ℏ c), where c is the speed of light, є0=1/µ0c2 is the permitivity of vacuum, and µ0 is the permeability of vacuum. In the International System of Units (SI), c, є0, and µ0 are exactly known constants. The optical transmittance of pristine graphene is defined as [65]
| T= | ⎛ ⎜ ⎜ ⎝ | 1+ |
| ⎞ ⎟ ⎟ ⎠ |
| ≈ 1−π α ≈ 0.977. (16) |
When scaled to its atomic thickness, graphene actually shows strong broadband absorption per unit mass of the material (π α=2.3%), which is ∼ 50 times higher than GaAs of the same thickness [64, 60, 66]. The reflectance under normal light incidence is relatively weak and written as R=0.25π 2α 2T= 1.3× 10−4, which is much smaller than the transmittance [60]. The absorption of few-layer graphene can be roughly estimated by scaling with the number of layers (T≅ 1−Nπ α). In principle, a low sheet resistance can be attained without sacrificing the properties of transparency too much (i.e., tens of Ω / ▫ for T>90%). As such, it is believed that few-layer graphene can potentially replace ITO (indium tin oxide) as transparent conductors for applications in solar cells [67, 68, 69] and touch screens [70, 71, 72] in cases when it is sufficiently doped [65].
Based on the exciting optical properties of graphene, many graphene-based photonic and optoelectronic applications have been developed [70, 73, 74]. In this thesis we study the application of graphene-based structures as photodetectors (Fig. 2.6). Photodetectors measure the photon flux or optical power by converting the absorbed photon energy into electrical current [70]. They are used in various common devices in both science and technology [75], such as remote controls, televisions and DVD players. Modern light detectors are usually made using III-V semiconductors, such as gallium arsenide. When light strikes these materials, each absorbed photon creates an electron-hole pair (internal photoeffect). These pairs then separate and produce an electrical current. The spectral bandwidth is typically limited by the material’s absorption [75]. For example, photodetectors based on group IV and III-V semiconductors suffer from the ’long-wavelength limit’, as these become transparent when the incident energy is smaller than the bandgap [75]. A wide photon energy absorption range from the ultraviolet to terahertz could be covered by graphene-based photodetectors [60, 76, 77, 78]. The response time is ruled by the carrier mobility [75] which is huge in graphene and thus ultrafast photodetectors are feasible [70].
The photoelectrical response of graphene has been widely investigated both experimentally and theoretically [79, 80, 81, 82, 48]. A photoresponse up to 40 GHz is reported for graphene photodetectors in [82]. The operating bandwidth is mainly limited by the time constant resulting from the device resistance and capacitance. Xia et al. reported an RC-limited bandwidth of about 640 GHz [82], which is comparable to traditional photodetectors [83]. However, the maximum possible operating bandwidth of photodetectors is typically restricted by their transit time [75].
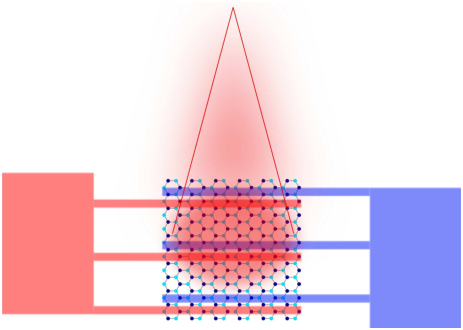
Figure 2.6: Schematic of a graphene photodetector.
The first application of graphene as a photodetector has been demonstrated in [84]. A detectable current has been reported that is attributed to the band bending at the metal/graphene interface [85]. Photocurrents have also been obtained at single/bilayer graphene interfaces [86] and graphene p-n junctions [87]. More recent studies concentrate on increasing the photoresponsivity of the graphene devices [88] and extending their operation range to longer wavelengths [89]. Recent photocurrent generation experiments in graphene show a strong photoresponse near metal/graphene interfaces, with an internal quantum efficiency of 15-30% despite its gapless nature [84, 81, 80]. Moreover, graphene photodetectors can potentially operate at speeds >500 GHz [82].
Although an external electric field can efficiently generate photocurrent with an electron-hole separation efficiency of over 30% [80], zero source-drain bias and dark current operations could be achieved by using the internal electric field formed near the metal electrode-graphene interfaces [82, 48]. However, the small effective area of the internal electric field could decrease the detection efficiency [82, 48], as most of the generated electron-hole pairs would be out of the electric field region, thus recombining, rather than being separated. The internal photocurrent efficiencies (15-30%; Refs [80, 82]) and external responsivity (generated electric current for a given input optical power) of ∼6.1 mA per Watt reported so far [48] are relatively low compared with current photodetectors [75]. This is mainly due to limited optical absorption when only one single layer graphene is used, short photocarrier lifetimes and small effective photodetection areas (∼200 nm in [82]).
Before the invention of diode lasers, a semiconductor laser based on transitions between Landau levels in a strong magnetic field was proposed by Lax in 1960 [90]. This is the first proposal of a semiconductor laser in which the optical transition occurs between low dimensional states of the same band (conduction or valence) rather than by the recombination of electron-hole pairs across the semiconductor bandgap [91]. The idea of a unipolar laser was then ignored for many years because only 2 years after the proposal of Lax the first diode laser was demonstrated [92]. This exploit drew all the attention of the semiconductor community on bandgap lasers and began the race for the first diode laser continuous-wave (cw) operation at room temperature. The race ended in 1970 when this goal was reached by the first AlGaAs/GaAs heterostructure laser at nearly the same time by Alferov’s group at the Ioffe Institute in St. Petersburg [93] and by Panish et al. [94] at Bell Labs (Murray Hill, NJ).
The effort to improve the performance of diode lasers and the development of the transistor technology in III-V compounds had an enormous impact on the epitaxial growth techniques of thin semiconductor layers and gave rise to the concept of two-dimensional structures such as quantum wells (QWs) and inversion layers [95]. The confinement of carriers in semiconductor quantum wells and superlattices leads to formation of energy levels and subbands. Figure 2.7 shows the conduction band of a quantum well which splits into subbands.
In 1970, Esaki and Tsu [96] proposed the use of heterostructures for applications in optoelectronics. Kazarinov and Suris [97] were the first to propose intersubband transitions to design a laser. The quantum cascade laser (QCL) is a special kind of semiconductor laser, usually emitting mid-infrared light. Such a laser operates on laser transitions not between different electronic bands, but instead on intersubband transitions of a semiconductor structure. The first QCL was demonstrated by Federico Capasso in 1994 at Bell Labs for a wavelength of 4.2 µ m, [98] and in 2001 Alessandro Tredicucci developed the first MIR QCL, operating at 68 µ m [99]. QCLs have since then achieved significant performance improvements and are poised to become the dominant laser sources in the mid- and far-infrared spectral ranges. Lasing has been obtained at wavelengths ranging from 3.4-24 µ m [98, 100] in the mid-infrared and 60-161 µ m in the far-infrared [101].
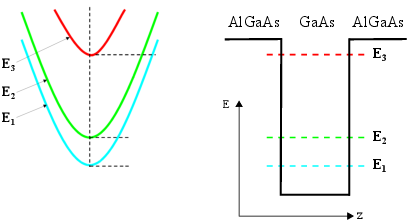
Figure 2.7: Subbands in a quantum well. The potential well caused by the AlGaAs/GaAs layer structure gives rise to bound states localized in the well. In k-space, there exist continuous subbands as the electrons are not confined in the plane of the well.
The general principles of QCL operation are illustrated in Fig. 2.8. Shown are two active regions, i.e. the quantum well and barrier regions that support the electronic states between which the laser transition is taking place, and schematically the intermediate injector region. We draw the conduction band edge of the InGaAs QWs and the AlInAs barriers using the 520 meV low-temperature conduction band-offset usually associated with the materials’ compositions (In0.53Ga0.47As, Al0.48In0.52As) lattice matched to the InP substrate. An external electric field is applied as visualized by the linear slope of the electronic potential. Solving the Schrödinger equation results in the energy levels drawn and the moduli squared of the wave functions. The wave functions and energy levels of each stage are shown. The lasing subbands are indicated with bold solid/bold dashed lines.
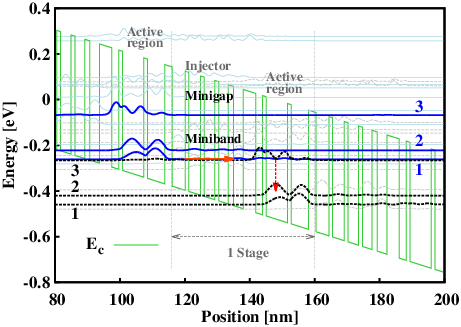
Figure 2.8: Schematic conduction band energy diagram of two QCL active regions with the intermediate injector region and the moduli squared of the wave functions involved in the laser transition (labelled 1, 2, and 3). The laser transition is indicated by the vertical arrow, the electron flow by the horizontal arrow.
The QW thicknesses in the active region are selected such that the energy separation between level 3 and 2 corresponds to the desired wavelength. The energy separation between level 2 and 1 is deliberately chosen to be very close to the energy of the LO-phonon modes of the InGaAs/AlInAs/active region materials. Under an appropriate applied bias, electrons tunnel from the injector region into energy level 3, the upper laser state, of the active region. Electrons scatter from this level into both lower-lying levels 2 and 1, very rapidly emitting LO-phonons. The scattering time between levels 2, the lower laser state, and level 1 is ultra-short due to the resonant nature of this transition with the LO-phonon. Therefore, population inversion occurs between the laser levels 3 and 2 and laser action is possible. Electrons need only be supplied fast enough into level 3 by tunneling from the preceding injector region, and need to exit from levels 2 and more so from level 1 into the following downstream injector region at a high rate by tunneling. Inside the injector region and brought about by the externally applied electric field, electrons gain again in energy (relative to the band bottom) and are injected into the following downstream active region.
Typical QCLs have a cascade containing 20 to 30 active regions alternated with injector regions, although laser action has been achieved for a single active region [102], and has been tested for as many as 100 active regions [103]. A key feature of QCLs is the ability to cascade N modules together, so that a single injected electron can emit many photons, which allows for a differential quantum efficiency greater than unity.
In QCLs, three aspects mainly influence laser performance. First of all, optimization of the active region design, in order to ensure efficient carrier injection in the upper lasing state and carrier extraction out of the lower lasing state. Second, epitaxial growth optimization and third, optimization of the fabrication process, which is crucial to reduce optical losses and improve the laser thermal conductance [104]. Concerning the optimization of the laser design, many schemes have been proposed [105, 106, 107], however, a systematic study of the laser design was never permitted due to the large number of variables involved [104].
Since their inception in 1994 many designs of QCLs have emerged, and can basically be characterized by their number of QWs in the active region and the spatial extent and number of the wave functions in the active regions [108]. Three high-performance structures are introduced in the following.
The structure discussed in the last section (Fig. 2.8) is called a three-well (3QW) vertical-transition QCL in which a thin well is inserted between the injector region and an active region (which could also be termed a two-well vertical-transition active region). The additional QW leads to a significant reduction of electron scattering (leakage) from the injector directly into the laser ground state 2 and also level 1 [108]. The improvement led to the first high-performance, room temperature operation of QCLs [109]. This laser design, emitting at 8µ m wavelength, provides high optical gain and concomitant robust laser action [110].
The active region, shown in Fig. 2.8, consists of three InGaAs QWs closely coupled by thin InAlAs barriers. At the appropriate electric field, corresponding to the measured laser threshold, the upper laser level (level 3) is separated from the lower laser level (level 2). The lower laser level is closely coupled to the ground state (level 1) of the active region, such that the two levels are strongly anti-crossed. This increases the matrix element z32 with respect to z31 and maximizes the scattering time between levels 3 and 2 with respect to the scattering time between levels 3 and 1. The energy difference between levels 2 and 1, designed to efficiently deplete the lower laser level of electrons via resonant LO-phonon scattering.
The injector ’miniband’ — more accurately, the manifold of energy levels in the injector — has been designed to be ’flat’. Its ground level is located below the upper laser level. Even the next-higher level of the injector miniband is energetically lower than the upper laser level. The injector has been doped in the center part. Therefore, at laser threshold, electrons are not injected from the Fermi-surface into the upper laser level. Furthermore level 1 of the preceding active region is in resonance with level 3 of the following active region, allowing for resonant carrier transport between successive active regions without significant carrier relaxation in the injector. In comparison, the relaxation time within the injector is long since the energy separation to the adjacent lower energy level is well below the LO-phonon energy and the ground level of the injector region is partly filled with electrons.
The 3QW vertical-transition design has this advantage that it avoids a too early ’shut-down’ of the laser due to suppression of resonant tunneling [111]. Once the electric field increases and the resonance between levels 1 and 3 is destroyed, there is still strong injection from the ground state of the injector, allowing for a wide dynamic range of current and concomitant high optical power [108]. The 3QW vertical-transition design is employed in the performance optimization and instability study presented in Sec. 6.2.
A different design of QCLs, which was first introduced in 1997, is the superlattice (SL) active region [112]. In short, laser action takes place between minibands, rather than between the subbands of few and single [113] well active region QCLs. High optical gain, large current carrying capabilities, and weaker temperature sensitivity are the advantages of SL-QCLs. However, they can generally only be applied for the longer-wavelength range (i.e. λ≥ 7µ m, for lattice-matched InP-based SL-QCLs) as the wider minibands take up more energy space than simple subbands [108].
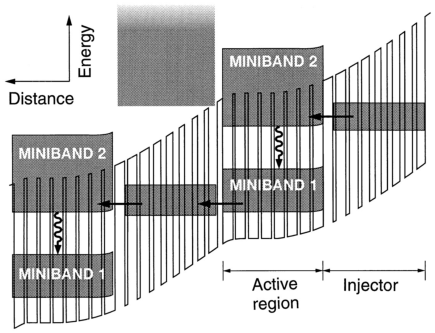
Figure 2.9: Conduction-band structure of the original SL-QCL. Two active region SLs with the preceding injector regions are shown. The minibands are indicated by gray regions. Laser action, as denoted by the wavy arrows, takes place across the first minigap 2-1. Adapted from [112].
In general, semiconductor SLs consist of a periodic stack of nanometer-thick layers of QWs and barriers. The period of this artificial crystal is typically much larger than the lattice constant of the bulk crystalline constituents. This superimposed periodic crystal potential splits the conduction band (and the valence bands as well) along the direction normal to the layers into a series of narrow (typically, tens to a few hundreds of meV wide) minibands separated by energy gaps (’minigaps’) in the strong-tunnel-coupling regime. For a given set of materials, miniband and minigap widths can be engineered by suitable choice of the layer thicknesses. In the generic case of the simple periodic SL, however, those widths are not independent of each other [108].
Figure 2.9 illustrates the original interminiband SL-QCL concept and its first realization [112]. Electrons are injected electrically from a preceding, equally doped, injector region directly into the ground state near the bottom of the second ’upper’ miniband, as was the case with the simple three-well active region discussed previously. From there, electrons can make an optical transition to the top of the lower miniband. In k-space, this transition occurs at the boundary of the mini-Brillouin-zone.
In QCLs, the inter-miniband scattering processes are generally dominated by LO-phonon emission. Specifically, an electron thermalized near the bottom of the higher miniband can relax down to states near the top of the lower miniband by scattering via LO-phonon emission employing a high momentum transfer. This process is characterized by a comparatively long scattering time of ∼ 10 ps. Within each miniband, the electrons relax much faster — in a few tenths of a picosecond — by intra-miniband scattering, because it involves the emission of small-wavevector optical phonons. The resulting large ratio of relaxation times of inter- versus intra-miniband scattering events ensures an intrinsic population inversion across the minigap [108].
A second unique design feature of the SL-QCL is the high oscillator strength for the optical transition at the mini-Brillouin zone boundary of the SL. The oscillator strength of radiative transitions between the first two minibands of a SL increases with wavevector and is maximum at the zone boundary [114]. In particular, it strongly increases with decreasing barrier thickness. In the original SL-QCL structure shown in Fig. 2.9, the wavelength was selected as 8 µm, using an eight-period SL with 1 nm thick AlInAs barriers and 4.3 nm thick InGaAs QWs in lattice-matched composition. The structure was optimized for maximum oscillator strength with an optical dipole matrix element of 3.6 nm, i.e. approximately twice as large as that of similar-wavelength QCLs featuring few-well active regions.
The third type of active region we discuss here is called ’diagonal’ transitions active region in which the upper and lower state wave functions are clearly located in spatially different regions. The 3QW and SL-QCLs designs described in the previous two sections had in common that the wavefunctions directly involved in laser action, i.e. the upper and lower laser state, are essentially located in the same region of real space.
The two wave functions being collocated has several distinctive consequences. First, from an energy level point of view, the energy separation of the two states is largely independent of the applied electric field in a fairly wide range around the design field. This gives lasers based on such a vertical design a clear robustness in terms of wavelength versus applied voltage and, as a consequence, also versus temperature. On the other hand, and relating to the calculation of the gain coefficient, the collocation of the wave functions leads to a comparatively large optical dipole matrix element, but also comparatively short electron scattering times. Both are a result of the large overlap of the wave functions of upper and lower laser states [108].
In contrast to 3QW vertical transitions, QCLs based on such active regions show a strong dependence of the wavelength on the applied electric field through a voltage-induced Stark effect. The design parameters are furthermore characterized through a smaller dipole matrix element but also clearly longer scattering times, thus allowing again for sufficient gain to achieve laser action [108]. These lasers can operate up to room temperature and are exploited for large wavelength tunability [115]. This particular design can be used to fabricate QCLs that operate under both bias polarities and with nearly independent attributes, such as two different wavelengths [116] depending on bias polarity.
Ultrashort pulses with large instantaneous intensities from mode-locked lasers are key elements for many important applications such as time-resolved measurements [117, 118], optical parametric generation [119], coherent control [120], four-wave mixing [121], and frequency combs [122].
The word mode-locking describes the locking of multiple axial modes in a laser cavity. By enforcing coherence between the phases of different modes, pulsed radiation can be produced. Mode-locking is a resonant phenomenon. By a relatively weak modulation synchronous with the roundtrip time of radiation circulating in the laser, a pulse is initiated and can be made shorter on every pass through the resonator. The shortening process continues unabated, until the pulse becomes so short and its spectrum so wide that pulse lengthening mechanisms or spectrum narrowing processes spring into action, such as finite bandwidth of the gain. The history of laser mode-locking is a progression of new and better ways to generate shorter and shorter pulses, and of improvements in the understanding of the mode-locking process.
To date, the most common approach to generate short pulses in the mid-infrared molecular "fingerprint" region relies on the down-conversion of short-wavelength mode-locked lasers through nonlinear processes. These systems are usually bulky, expensive and typically require a complicated optical arrangement [123]. Design degrees of freedom in QCLs such as emission wavelength, gain spectrum [124], carrier transport characteristics, and optical dispersion make the QCL a unique candidate to serve as a semiconductor source of ultra-short pulses at MIR and THz domains. There is, however, an obstacle of fundamental origin that has so far prevented achieving ultrashort pulse generation in QCLs [125, 126]. In intersubband transitions, the carrier relaxation is extremely fast because of optical phonon scattering. As a result, the gain recovery time in QCLs, determined both by upper state lifetime and by the electron transport through the cascade heterostructure, is typically on the order of a few picoseconds [127] which is an order of magnitude smaller than the cavity roundtrip time of 40-60 ps for a typical 2-3 mm-long laser cavity [123]. According to conventional mode-locking theory, this situation prevents the occurrence of stable passive mode-locking. However, under these conditions the elusive Risken-Nummedal-Graham-Haken (RNGH)-like instability can be possible in QCLs [125].
A saturable absorber is an optical component with a certain optical loss, which is reduced at high optical intensities. This can occur, e.g., in a medium with absorbing dopant ions, when a strong optical intensity leads to depletion of the ground state of these ions. Similar effects can occur in semiconductors, where excitation of electrons from the valence band into the conduction band reduces the absorption for photon energies just above the bandgap energy. The main applications of saturable absorbers are passive mode locking and Q switching of lasers, i.e., the generation of short pulses. However, saturable absorbers are also useful for purposes of nonlinear filtering outside laser resonators, e.g. for cleaning up pulse shapes, and in optical signal processing. In lasers with a relatively long gain recovery time compared to the cavity round-trip time, the instability caused by a saturable absorber (SA) can often lead to passive mode locking [128].
We investigate the passive mode locking with saturable absorber in QCLs operating at MIR and THz. The effects of saturable absorber and pumping strength on the instability characteristics are studied. A numerical calculation based on the Maxwell-Bloch equations is performed to analyze the dynamics of QCLs, see Sec. 6.3.
In this work, we analyze the optical properties of semiconductor nanostructures and their application in photodetectors and lasers. Graphene with various geometrical structures embedded in boron-nitride lattices is studied as a new material. Quantum cascade lasers and detectors are studied in this thesis.
Chapter 3 investigates the optical properties of armchair graphene nanoribbons (AGNRs) and graphene nanoribbons embedded in boron nitride (BN) lattices. The first principle calculations, the tight-binding model, and the non-equilibrium Green’s function formalism employed in this study are presented in Sec. 3.1. In Sec. 3.2, the optical matrix elements and transition rules are discussed. Dielectric response, quantum efficiency, and photoresponsivity of AGNRs/BN are discussed in Sec. 3.3. Finally, Sec. 3.4 provides concluding remarks for this chapter.
Chapter 4 describes the analytical approach to approximate the wave functions and energy dispersion in zigzag graphene nanoribbons (ZGNRs). The electronic structure of ZGNRs is derived analytically in Sec. 4.1. The wavenumber approximations to reach analytical models for the dispersion relation and the wave function are derived in Sec. 4.2. In Sec. 4.3, optical matrix elements and transition rules of ZGNRs are obtained from the model. The two approximations used in our models and the derived optical properties are discussed in Sec. 4.4. Finally, Sec. 4.5 draws concluding remarks for this chapter.
In chapter 5, graphene superlattice-based photodetectors are discussed. The optical properties of one dimensional superlattices formed by AGNRs embedded in BN superlattices are presented in Sec. 5.1. The line-edge roughness model is described in Sec. 5.2. This chapter is concluded in Sec. 5.3.
In Chapter 6, the application of quantum cascade structures for the MIR and terahertz region is discussed. An optimization and dynamics study of quantum cascade lasers (QCLs) is presented. Section. 6.1 describes the transport and optimization models. In Sec. 6.2, the simulation results for performance optimization are presented and discussed. Dynamics of QCLs is studied in Sec. 6.3. Quantum cascade detectors are presented in Sec. 6.4.
Chapter 7 finally summarizes the thesis with conclusions.


