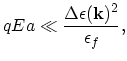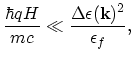2. The Semiclassical Transport Model
The semiclassical transport model represents a generalization of the theory of free electrons in the case of a spatially-periodic potential. In the
free electron theory electrons move between two collisions according to the classical equations of motion. From the quantum mechanical point of view
these equations of motion actually describe the behavior of wave packets constructed using energy levels of a free electron. This can be generalized for
the case of electrons in an arbitrary periodic potential where plane waves are replaced by Bloch's waves. The proof of this generalization is a
difficult mathematical task. However it removes various contradictions of the free electron theory. In particular, in the semiclassical model electron
collisions with motionless periodic ions do not influence the resistivity of a solid because now the electron interaction with fixed periodic lattice has
been
taken into account in the original Sroedinger's equation which Bloch's wave is obtained from. In other words, within Bloch's theory the classical point of
view about scattering on fixed periodic ions is not valid any longer. From the quantum mechanical point of view this means that in a periodic structure of
scattering centers a wave can move without any damping [14].
The semiclassical model based on the concept of Bloch's wave packets correctly works only when the electron position is measured with an accuracy of the
wave packet width. The fact that the wave packet width must be less than the size of the Brillouin zone can be used to estimate the size of Bloch's wave
packets and the limitations of the semiclassical model. Similar to the theory of free electrons, the wave packet is constructed using energy levels of
an electron. But now an electron is represented by Bloch's wave:
 |
(2.1) |
where  numerates bands and
numerates bands and
 for
for
 . Changing the position of an electron from
. Changing the position of an electron from  to
to
 , where
, where  is a Bravais lattice vector, gives:
is a Bravais lattice vector, gives:
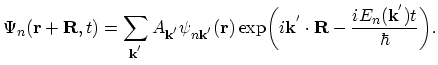 |
(2.2) |
As a function of  this expression is just a superposition of plane waves with another weight. Thus the wave packet must be localized in a domain
with a characteristic size
this expression is just a superposition of plane waves with another weight. Thus the wave packet must be localized in a domain
with a characteristic size
 . The characteristic size
. The characteristic size  is less than the size of the Brillouin zone which is of the
order of
is less than the size of the Brillouin zone which is of the
order of  , where
, where  is the lattice constant. This gives the condition
is the lattice constant. This gives the condition
 , that is, the wave packet built from Bloch energy levels and
which has a wave vector correctly determined in a domain smaller than the size of the Brillouin zone is smeared over a large number of elementary crystal
cells in the coordinate space. Therefore the conclusion is that the semiclassical model describes the electron response to external electric and magnetic
fields which slowly change within the wave packet's width and thus more slowly within an elementary cell. In this model such fields are responsible for
the creation of classical forces which determine the evolution of the wave packet's coordinate and its wave vector.
, that is, the wave packet built from Bloch energy levels and
which has a wave vector correctly determined in a domain smaller than the size of the Brillouin zone is smeared over a large number of elementary crystal
cells in the coordinate space. Therefore the conclusion is that the semiclassical model describes the electron response to external electric and magnetic
fields which slowly change within the wave packet's width and thus more slowly within an elementary cell. In this model such fields are responsible for
the creation of classical forces which determine the evolution of the wave packet's coordinate and its wave vector.
It should be noted that the semiclassical model is more complex than the classical limit of free electrons. This difference comes from the fact that the
characteristic length at which the lattice periodic potential considerably changes is smaller than the wave packet's width and thus this potential cannot
be treated classically. Consequently, the semiclassical model represents only in part the classical limit as the external fields are only considered
classically while the ion periodic field is treated quantum mechanically.
An additional element of the quantum mechanical nature of the semiclassical model is that the electron wave vector is only accurate to the vector
 of the reciprocal lattice. Thus two sets of variables
of the reciprocal lattice. Thus two sets of variables
 and
and
 specify the same electron
state.
This means that all physically distinguishable wave vectors within the same band are located within the elementary cell of the reciprocal lattice.
specify the same electron
state.
This means that all physically distinguishable wave vectors within the same band are located within the elementary cell of the reciprocal lattice.
The fact that in the semiclassical model the band number represents an integral of motion allows to formulate some restrictions on the external
fields.
For the amplitude of the electric field  the condition reads:
the condition reads:
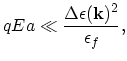 |
(2.3) |
and for the amplitude of the magnetic field  the condition has a similar form:
the condition has a similar form:
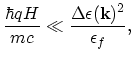 |
(2.4) |
where
 and
and
 is the Fermi energy. The frequency of the external
electromagnetic field must satisfy the following condition:
is the Fermi energy. The frequency of the external
electromagnetic field must satisfy the following condition:
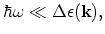 |
(2.5) |
which prevents that a photon with a high enough energy causes an interband transition. For the wave length of the external electromagnetic field the
condition
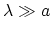 |
(2.6) |
is necessary to make the concept of wave packets meaningful.
Subsections
S. Smirnov:

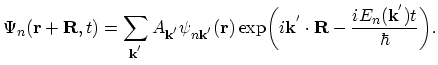
![]() of the reciprocal lattice. Thus two sets of variables
of the reciprocal lattice. Thus two sets of variables
![]() and
and
![]() specify the same electron
state.
This means that all physically distinguishable wave vectors within the same band are located within the elementary cell of the reciprocal lattice.
specify the same electron
state.
This means that all physically distinguishable wave vectors within the same band are located within the elementary cell of the reciprocal lattice.
![]() the condition reads:
the condition reads: